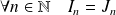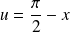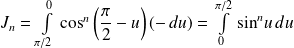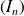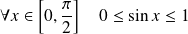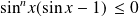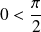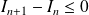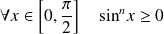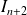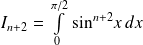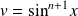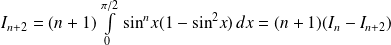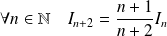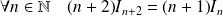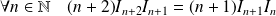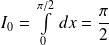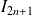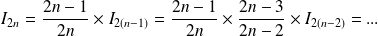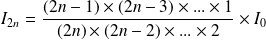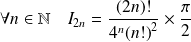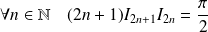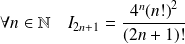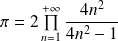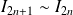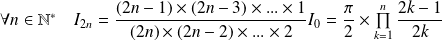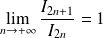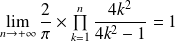Intégration d'une fonction numérique

Exo 12

Commencez par chercher à résoudre l'exercice par vous-même.

Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.

Une solution détaillée vous est ensuite proposée.

Soit un entier naturel. On définit les intégrales : et .

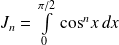Question

Démontrer que : .

Indice

Faites un changement de variable.

Solution

On effectue dans le changement de variable .

.

Conclusion : .

Remarque

Dans la suite de l'exercice, on ne s'intéressera donc qu'à la suite .

Ces intégrales sont appelées les intégrales de Wallis.

Question

Démontrer que la suite est convergente.

Indice

Démontrez que la suite est monotone et bornée.

Solution

On étudie le sens de variations de la suite : .

, donc : . Et , donc : .

Donc la suite est décroissante et minorée par car : .

Conclusion : La suite est convergente.

Question

Déterminer une relation entre et . En déduire une relation entre et .

Indice

Intégrez par parties.

Solution

On intègre par parties en posant : et .

.

Donc : .

Conclusion : .

, donc : .

Donc la suite de terme général est stationnaire (constante).

Donc : .

Or : et : .

Conclusion : .

Question

En déduire la limite de la suite et un équivalent de 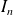quand tend vers l'infini.

Indice

Utilisez la relation entre 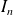et .

Solution

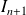Soit 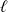la limite de la suite . Donc : .

Conclusion : La suite converge vers .

La suite est décroissante, donc : 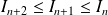, donc : .

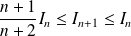L'intégrale 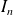n'est pas nulle car la fonction 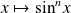garde un signe constant et n'est pas identiquement nulle sur l'intervalle .

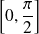Donc : . Or : 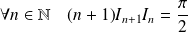, donc : .

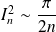Conclusion : .

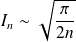Question

Déterminer l'expression de et de en fonction de .

Indice

Utilisez la relation entre et .

Solution

En itérant, on obtient : .

Donc : .

Conclusion : .

Et : , donc : .

Conclusion : .

Question

En déduire la formule de Wallis : .

Indice

Remarquez que : .

Solution

On a montré que : .

Et : .

Or : . Donc : .

Donc : .

Conclusion : .

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimer Paternité - Pas d'Utilisation Commerciale - Partage des Conditions Initiales à l'IdentiqueRéalisé avec Scenari (nouvelle fenêtre)