Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
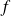la fonction définie sur
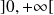par :
.
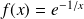Question
Démontrer que la fonction
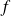est prolongeable par continuité en
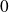et que son prolongement par continuité est de classe
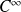sur
.
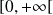Déterminez les dérivées successives de la fonction
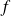et leurs limites en
.
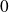Utilisez le théorème de prolongement des fonctions de classe
.
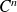La fonction
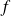est composée de la fonction
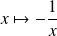qui est de classe
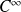sur
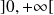et de la fonction exponentielle qui est de classe
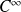sur
.
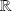Donc la fonction
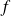est de classe
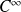sur
.
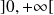Et :
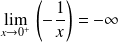. Donc :
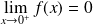. La limite est finie.
Donc la fonction
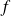est prolongeable par continuité sur
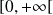en posant
.
,
, ...
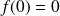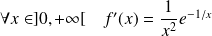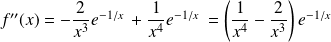Montrons par récurrence que, pour tout
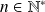, il existe un polynôme
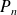tel que :
.
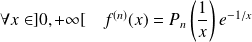Initialisation : D'après ce qui précède, on a
,
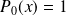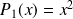et
.
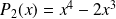Hérédité : Soit
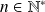pour lequel il existe un polynôme
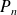tel que
.
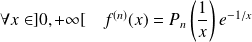Donc :
.
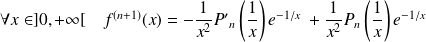Donc :
.
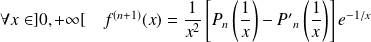Donc :
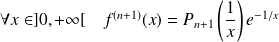en posant
.
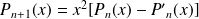La fonction
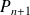est un polynôme puisque
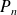et
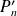le sont.
Conclusion : Pour tout entier
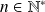, il existe un polynôme
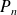tel que
.
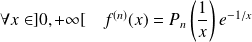Donc :
car
.
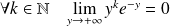Donc, pour tout
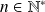, la fonction
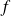est de classe
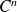sur
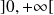et toutes ses dérivées admettent une limite finie en
.
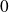Donc, pour tout entier
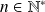, le prolongement de la fonction
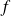est de classe
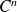sur
.
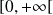Conclusion : Le prolongement par continuité de
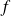est de classe
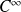sur
.
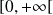