Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
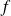la fonction définie par :
.
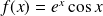Question
Pour tout entier
, déterminer la dérivée d'ordre
de la fonction
.
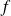Indice
Utilisez l'exponentielle complexe.
Solution
La fonction
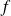est de classe
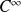sur
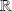comme produit de fonctions
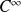sur
.
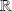On remarque que :
.
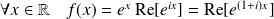Donc :
.
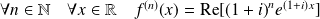Or :
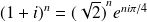. Donc :
.
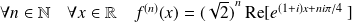Conclusion :
.
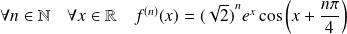Remarque :
On aurait pu utiliser la formule de Leibniz, mais les dérivées successives de la fonction cosinus étant, au signe près, soit sinus soit cosinus, on aboutirait à une expression beaucoup trop compliquée.
