Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Pour tout entier
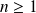 , on considère la fonction
, on considère la fonction
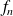 définie par :
définie par :
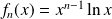 .
.
Question
Déterminer la dérivée d'ordre
 de la fonction
de la fonction
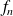 .
.
Il y a deux solutions :
soit vous conjecturez une formule en examinant les premiers termes, puis vous raisonnez par récurrence.
soit vous utilisez la formule de Leibniz.
Première solution
La fonction
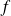 est de classe
est de classe
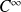 sur
sur
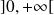 comme produit de fonctions de classe
comme produit de fonctions de classe
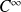 .
.
Pour
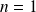 :
:
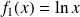 , donc
, donc
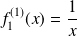 .
.
Pour
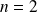 :
:
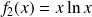 , donc
, donc
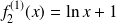 et
et
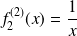 .
.
Pour
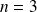 :
:
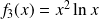 , donc
, donc
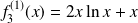 ,
,
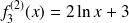 et
et
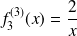 .
.
Pour
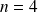 :
:
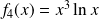 , donc
, donc
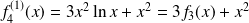 , et
, et
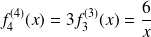 .
.
On conjecture que :
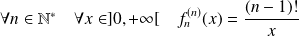 .
.
On le démontre par récurrence.
Initialisation : Elle est déjà faite.
Hérédité : Soit
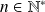 tel que
tel que
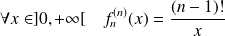 .
.
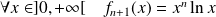 , donc :
, donc :
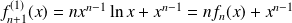 .
.
La dérivée
 -ième d'un polynôme de degré
-ième d'un polynôme de degré
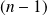 est nulle.
est nulle.
Donc :
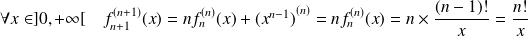 .
.
Conclusion :
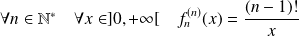 .
.
Deuxième solution
On utilise la formule de Leibniz :
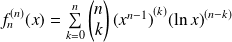 .
.
Or :
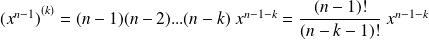 si
si
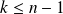 et
et
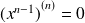 .
.
Et :
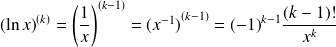 si
si
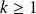 .
.
Donc :
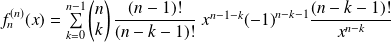 .
.
Donc :
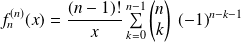 .
.
Or :
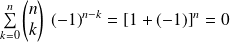 , donc :
, donc :
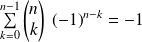 et
et
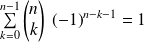 .
.
Conclusion :
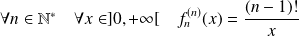 .
.





