Dérivées successives
Les dérivées successives se définissent par récurrence.
Soit
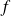une fonction définie sur un intervalle
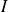de
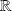et à valeurs réelles ou complexes.
Définition :
On note :
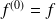et
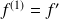si la fonction
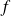est dérivable.
Pour tout entier
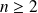, une fonction
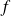est
fois dérivable si
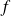est
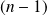fois dérivable et si sa dérivée
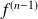est dérivable.
Alors :
.
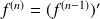La dérivée seconde
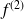est aussi notée
.
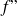Fondamental :
Opérations
Soient
et
deux fonctions
fois dérivables sur un intervalle
.
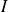La fonction
est
fois dérivable sur
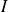et :
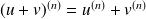.Si
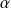est une constante, la fonction
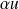est
fois dérivable sur
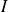et :
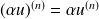.La fonction
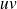est dérivable sur
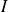et :
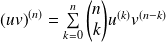(Formule de Leibniz).Si la fonction
ne s'annule pas, la fonction
est
fois dérivable sur
.
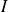Mais, pour le quotient, il n'y a pas de formule simple à retenir.
Fondamental :
Composition
Si la fonction
est
fois dérivable sur un intervalle
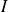et si la fonction
est
fois dérivable sur l'intervalle
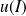, alors la fonction
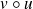est
fois dérivable sur
.
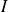Mais, pour la composition non plus, il n'y a pas de formule simple à retenir.
Définition :
Classes de fonctions
Une fonction
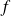est de classe
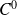sur un intervalle
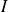si
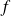est continue sur
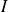.Une fonction
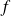de classe
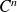sur un intervalle
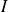si
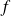est
fois dérivable sur
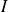et si
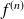est continue sur
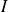.Une fonction
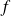de classe
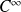sur un intervalle
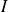si
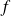est indéfiniment dérivable sur
.
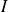Les ensembles
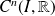et
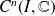des fonctions de classe
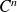sur un intervalle
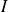sont des espaces vectoriels.
Les ensembles
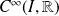et
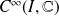des fonctions de classe
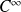sur un intervalle
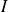sont des espaces vectoriels.
Fondamental :
Prolongement des fonctions de classe Cn
Si
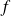est une fonction continue sur
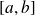, de classe
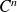sur
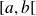et si toutes ses dérivées admettent des limites finies en
:
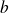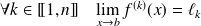, alors la fonction
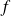est de classe
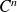sur
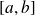et
.
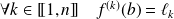