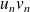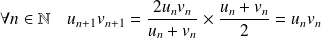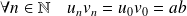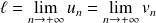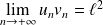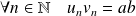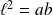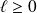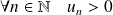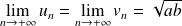Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
 et
et
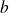 deux réels tels que
deux réels tels que
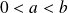 .
.
On définit deux suites
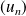 et
et
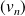 par
par
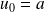 et
et
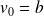 , et les relations :
, et les relations :
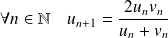 et
et
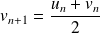 .
.
Question
Etudier le sens de variations des suites
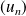 et
et
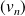 .
.
Commencez par démontrer que :
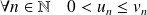 .
.
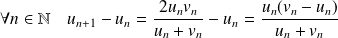 .
.
Et :
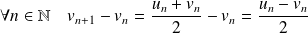 .
.
Montrons par récurrence que :
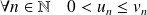 .
.
Initialisation :
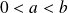 , donc :
, donc :
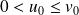 .
.
Hérédité : Soit
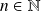 tel que
tel que
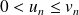 .
.
Donc :
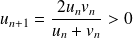 et
et
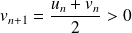 .
.
De plus :
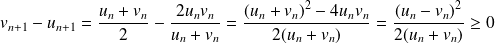 .
.
Donc :
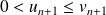 .
.
Conclusion :
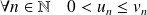 .
.
Donc :
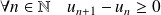 et
et
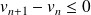 .
.
Conclusion : La suite
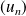 est croissante et la suite
est croissante et la suite
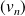 est décroissante.
est décroissante.
Question
Démontrer que :
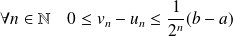 .
.
En déduire que les suites
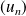 et
et
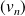 sont convergentes.
sont convergentes.
Démontrez que les suites
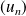 et
et
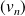 sont adjacentes.
sont adjacentes.
On raisonne par récurrence.
Initialisation :
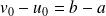 , donc :
, donc :
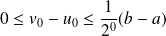 .
.
Hérédité : Soit
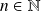 tel que
tel que
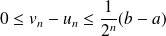 .
.
On a vu que :
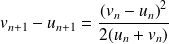 , donc :
, donc :
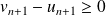 .
.
Et :
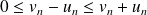 puisque
puisque
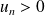 . Donc :
. Donc :
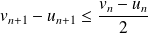 .
.
Or :
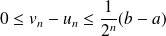 . Donc :
. Donc :
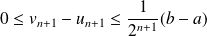 .
.
Conclusion :
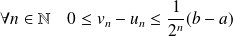 .
.
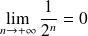 , donc d'après le théorème d'encadrement :
, donc d'après le théorème d'encadrement :
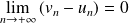 .
.
De plus les suites
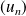 et
et
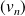 sont monotones de sens contraires, donc elles sont adjacentes.
sont monotones de sens contraires, donc elles sont adjacentes.
Conclusion : Les suites
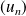 et
et
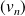 sont convergentes et elles admettent la même limite.
sont convergentes et elles admettent la même limite.