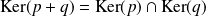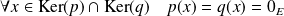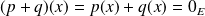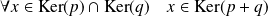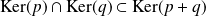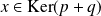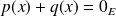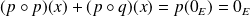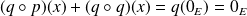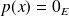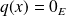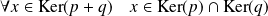Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
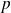 et
et
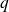 deux projecteurs d'un espace vectoriel
deux projecteurs d'un espace vectoriel
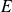 .
.
Question
Montrer que
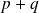 est un projecteur si et seulement si
est un projecteur si et seulement si
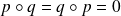 .
.
Démontrez d'abord que
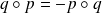 .
.
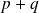 est un endomorphisme, donc
est un endomorphisme, donc
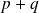 est un projecteur si et seulement si :
est un projecteur si et seulement si :
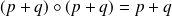 .
.
Or
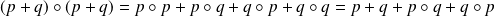 car
car
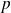 et
et
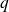 sont des projecteurs, donc
sont des projecteurs, donc
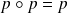 et
et
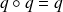 .
.
Donc
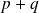 est un projecteur si et seulement si :
est un projecteur si et seulement si :
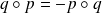 .
.
Donc, si
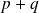 est un projecteur, alors :
est un projecteur, alors :
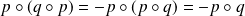 . Or
. Or
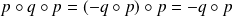 .
.
Donc, si
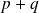 est un projecteur, alors :
est un projecteur, alors :
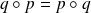 . Or
. Or
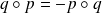 . Donc
. Donc
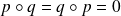 .
.
Réciproquement, si
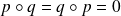 , alors
, alors
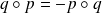 , donc
, donc
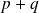 est un projecteur
est un projecteur
Conclusion :
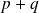 est un projecteur si et seulement si
est un projecteur si et seulement si
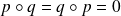 .
.
Question
Si
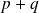 est un projecteur, montrer que :
est un projecteur, montrer que :
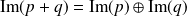 .
.
Démontrez d'abord l'égalité de la somme par double inclusion.
Puis démontrez que la somme est directe.
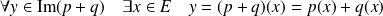 .
.
Donc
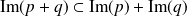 .
.
Réciproquement, soit
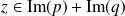 . Donc
. Donc
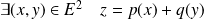 .
.
Donc par linéarité :
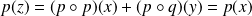 car
car
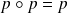 et
et
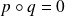 .
.
De même :
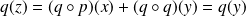 car
car
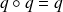 et
et
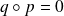 .
.
Donc
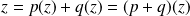 , donc
, donc
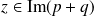 . Donc
. Donc
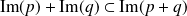 .
.
Donc
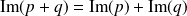 .
.
Soit
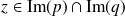 . Donc
. Donc
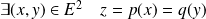 .
.
Donc
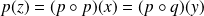 . Donc
. Donc
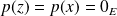 car
car
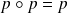 et
et
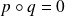 . Donc
. Donc
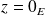 .
.
Donc
 .
.
Conclusion : Si
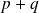 est un projecteur, alors
est un projecteur, alors
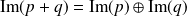 .
.