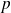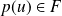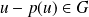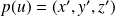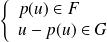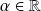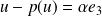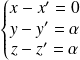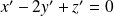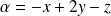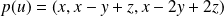Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Montrer que
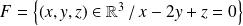et
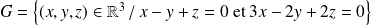sont des sous-espaces vectoriels supplémentaires de
.
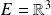Indice
Montrez que
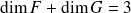et
.
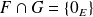Solution
Un vecteur
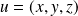appartient à
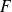si et seulement si
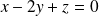, donc si
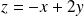, donc si
.
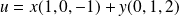Donc
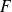est le plan vectoriel de base
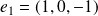et
.
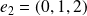Un vecteur
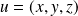appartient à
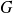si et seulement si
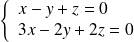, donc si
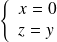, donc si
.
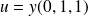Donc
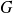est la droite vectorielle de base
.
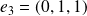Donc
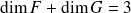et
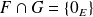car
.
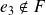Conclusion :
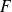et
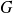sont des sous-espaces vectoriels supplémentaires de
.
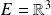