Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
un ensemble,
et
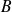deux parties de
.
Soit
l'application de
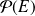dans
qui à toute partie
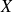de
associe
.
Question
Démontrer que l'application
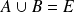est injective si et seulement si
.
est injective si et seulement si
.
Et pour toutes parties
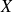et
d'un ensemble
:
.
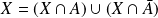Montrons successivement les deux implications.
Supposons que
est injective.
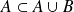donc
. De même
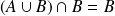. Donc :
.Or :
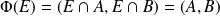. Donc :
.Or
est injective, donc :
.
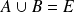Supposons que
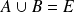.Soient
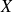et
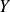deux parties de
telles que
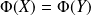, donc :
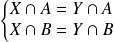.Donc :
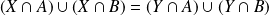. Donc :
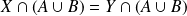.Or :
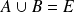. Donc :
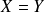. Donc
est injective.
Conclusion : L'application
est injective si et seulement si
.
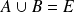Question
Démontrer que
est surjective si et seulement si
.
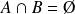Dans l'une des implications, utilisez un antécédent de
.
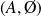Dans l'autre, traduire
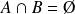en termes de complémentaires.
Montrons successivement les deux implications.
Supposons que
est surjective.Donc pour tout
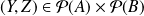, il existe
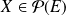tel que
.En particulier, il existe
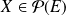tel que
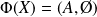, donc :
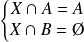.Donc :
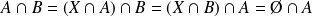. Donc :
.
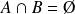Supposons que
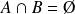. Donc :
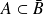et
.Soit
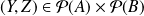. Donc :
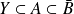et
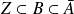.Donc :
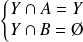et
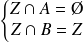. Donc :
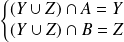.Donc :
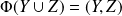. Donc :
. Donc
est surjective.
Conclusion :
est surjective si et seulement si
.
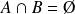Question
En déduire à quelle condition
est bijective, et déterminer alors son application réciproque.
est bijective si et seulement si elle est injective et surjective, donc si et seulement si
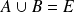et
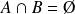, donc si et seulement si
.
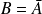Conclusion : L'application
est bijective si et seulement si
et
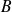sont complémentaires.
Et d'après la deuxième question, si
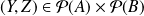, alors
.
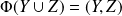Conclusion : L'application réciproque de
est l'application qui à tout
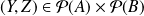associe
.
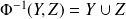