Exo 6
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
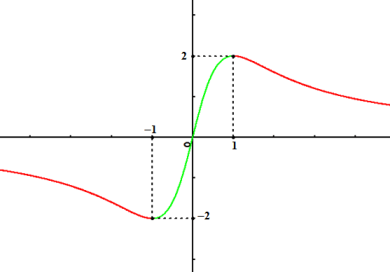
Montrer que l'application
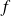 définie sur
définie sur
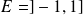 par :
par :
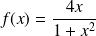 est bijective de
est bijective de
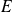 dans une partie
dans une partie
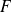 de
de
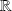 que l'on déterminera.
que l'on déterminera.
Préciser son application réciproque.
Cherchez à quelle condition un élément
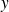 de
de
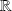 a un antécédent unique dans
a un antécédent unique dans
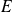 .
.
Cherchons les antécédents d'un réel
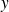 :
:
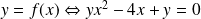 .
.
Si
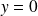 , l'équation devient :
, l'équation devient :
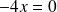 . Donc
. Donc
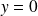 a un unique antécédent
a un unique antécédent
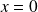 car
car
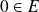 .
.
Si
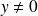 , on a une équation du second degré de discriminant
, on a une équation du second degré de discriminant
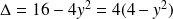 .
.
Si
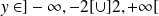 , alors
, alors
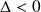 , donc l'équation n'a pas de solution, et donc
, donc l'équation n'a pas de solution, et donc
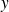 n'a pas d'antécédent.
n'a pas d'antécédent.
Si
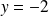 , alors
, alors
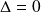 , donc l'équation a une seule solution
, donc l'équation a une seule solution
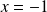 mais
mais
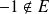 , donc
, donc
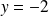 n'a pas d'antécédent dans
n'a pas d'antécédent dans
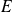 .
.
Si
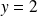 , alors
, alors
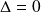 , donc l'équation a une seule solution
, donc l'équation a une seule solution
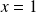 et
et
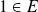 , donc
, donc
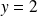 a un unique antécédent
a un unique antécédent
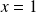 dans
dans
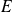 .
.
Si
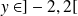 (et
(et
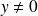 ), alors
), alors
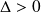 , donc l'équation a deux solutions distinctes. Notons
, donc l'équation a deux solutions distinctes. Notons
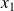 la plus petite et
la plus petite et
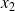 la plus grande. Voyons si elles appartiennent à
la plus grande. Voyons si elles appartiennent à
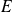 . Pour cela, introduisons le polynôme :
. Pour cela, introduisons le polynôme :
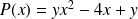 .
.
On a :
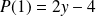 et
et
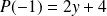 . Donc
. Donc
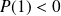 et
et
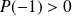
Si
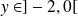 ,
,
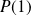 est du signe de
est du signe de
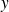 et
et
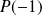 de signe contraire. Donc :
de signe contraire. Donc :
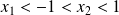 .
.
Et si
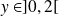 ,
,
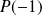 est du signe de
est du signe de
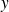 et
et
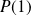 de signe contraire. Donc :
de signe contraire. Donc :
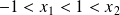 .
.
Donc dans les deux cas, une seule des solutions appartient à
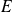 , et donc
, et donc
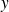 a un unique antécédent dans
a un unique antécédent dans
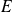 .
.
Donc un réel
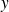 possède un unique antécédent dans
possède un unique antécédent dans
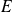 si et seulement si
si et seulement si
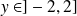 .
.
Conclusion : L'application
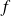 est bijective de
est bijective de
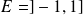 dans
dans
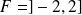 .
.
Sa réciproque
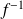 est l'application qui à tout
est l'application qui à tout
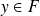 associe son unique antécédent.
associe son unique antécédent.
D'après ce qui précède :
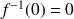 et
et
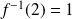 .
.
Si
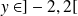 (et
(et
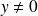 ), les racines du polynôme
), les racines du polynôme
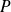 sont :
sont :
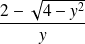 et
et
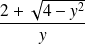 .
.
Si
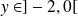 ,
,
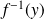 est la plus grande des deux racines. Donc :
est la plus grande des deux racines. Donc :
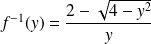 car
car
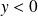 .
.
Si
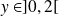 ,
,
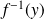 est la plus petite des deux racines. Donc :
est la plus petite des deux racines. Donc :
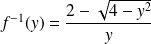 car
car
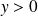 .
.
Conclusion :
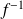 est l'application définie sur
est l'application définie sur
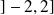 par :
par :
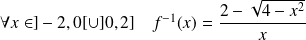 et
et
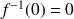 .
.





