Exo 7
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Soient
,
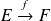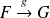et
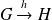trois applications.
Montrer que si
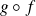et
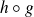sont bijectives, alors les applications
,
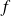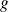et
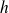sont bijectives.
Commencez par démontrer que
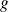est injective et surjective.
On suppose que
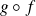et
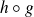sont bijectives.
Montrons que l'application
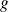est injective.Soient
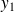et
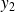deux éléments de
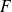tels que
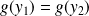.Donc :
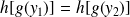, donc
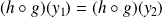.Or l'application
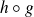est bijective, donc injective, donc
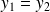.Donc l'application
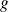est injective.
Montrons que l'application
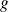est surjective.Soit
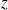un élément quelconque de
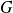.Or l'application
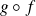est bijective, donc surjective de
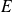dans
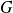.Donc il existe
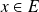tel que
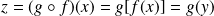en posant
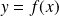.Donc, pour tout
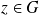, il existe
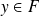tel que
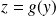.Donc l'application
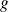est surjective.
Donc l'application
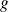est bijective. Soit
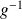sa réciproque.
Les applications
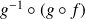et
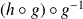sont composées de deux bijections, donc sont bijectives.
Or
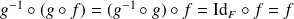et
.
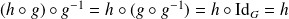Conclusion : Les applications
,
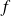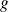et
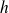sont bijectives.
