Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Soit
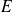 un ensemble non vide, et
un ensemble non vide, et
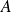 une partie non vide de
une partie non vide de
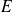 . On note
. On note
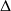 la différence symétrique.
la différence symétrique.
Montrer que l'application
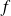 de
de
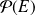 dans
dans
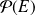 définie par :
définie par :
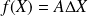 est bijective et préciser son application réciproque.
est bijective et préciser son application réciproque.
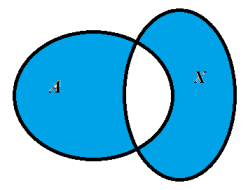
Cherchez le nombre de solutions de l'équation
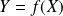 en étudiant l'intersection et la réunion de
en étudiant l'intersection et la réunion de
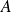 avec
avec
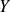 .
.
Soit
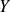 une partie de
une partie de
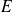 . Cherchons le nombre de solutions de l'équation
. Cherchons le nombre de solutions de l'équation
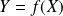 .
.
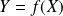 équivaut à :
équivaut à :
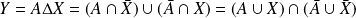 .
.
Donc si
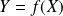 , alors :
, alors :
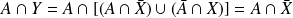 car
car
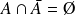 .
.
Et :
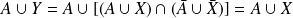 car
car
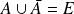 .
.
Donc :
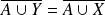 , donc :
, donc :
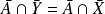 .
.
Or :
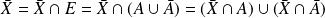 .
.
Donc si
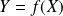 , alors :
, alors :
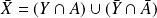 , donc
, donc
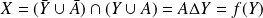 .
.
Donc l'équation
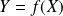 admet au plus une solution
admet au plus une solution
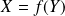 dans
dans
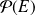 , et donc
, et donc
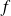 est injective.
est injective.
Et cette solution est bien un antécédent de
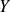 car si
car si
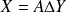 , alors :
, alors :
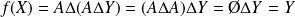 par associativité de la différence symétrique
par associativité de la différence symétrique
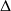 . Donc
. Donc
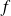 est surjective.
est surjective.
Conclusion : L'application
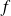 est bijective et sa réciproque est
est bijective et sa réciproque est
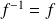 .
.





