Bijectivité
Définition :
L'application
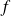est bijective si tout élément
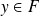possède un unique antécédent dans
.
Pour tout
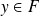, l'équation
possède une unique solution dans
.
Méthode :
Pour démontrer qu'une application
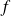de
dans
est bijective, on prend un élément
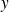quelconque dans
, et l'on cherche le nombre de solutions de l'équation
dans l'ensemble
.
Fondamental :
Propriétés :
-
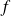est bijective de
dans
si et seulement si elle est injective et surjective.
Si
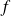et
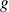sont bijectives, leur composée
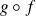est bijective.-
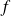est bijective de
dans
si et seulement si il existe une application
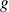de
dans
telle que
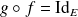et
.
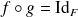Définition :
Si
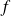est bijective de
dans
, on lui associe une application réciproque
de
dans
qui à tout élément de
associe son unique antécédent :
.
Méthode :
En résolvant l'équation
, l'expression de l'unique antécédent
en fonction de
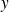donnera l'application réciproque.
Fondamental :
Propriétés :
Si
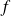est bijective de
dans
, son application réciproque
est bijective de
dans
.Si
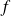est bijective de
dans
, alors :
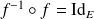et
.Si
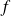et
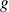sont bijectives,
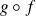est bijective et :
.
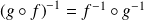