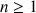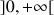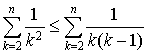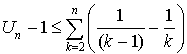Etude du comportement asymptotique d'une suite
La suite
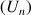est définie par 
.
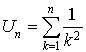Justifier que cette suite est convergente en démontrant qu'elle est croissante et majorée par 2 (la majoration par 2 sera obtenue à l'aide des relations : pour tout
, 
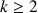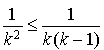et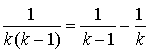 
).
