Comportement asymptotique : suite convergente ou divergente
Définition :
Par définition, dire que la suite
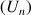, converge vers le réel
(
) signifie que, quel que soit l'intervalle ouvert
contenant
, cet intervalle
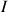contient tous les termes de la suite
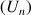à partir d'un certain rang ; le réel
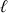est unique.
Les suites 
, 
, 
, ..., et les suites géométriques
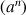avec
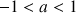sont les suites de références qui convergent vers 0.
Définition :
Par définition, dire que la suite
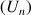diverge signifie que
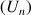vérifie l'un des 3 résultats suivants :
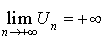, c'est-à-dire que tout intervalle du type
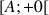contient tout les termes de
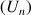à partir d'un certain rang.
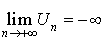, c'est-à-dire que tout intervalle du type
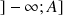contient tous les termes de la suite à partir d'un certain rang.La suite n'a pas de limite (par exemple la suite géométrique
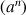avec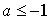 
).
Les suites 
,
,
,
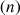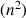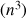, ..., et les suites géométriques
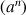avec
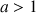sont les suites de référence qui divergent vers
.
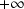Les suites ,
,
,
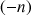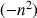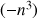, ..., sont les suites de référence qui divergent vers
.
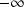