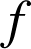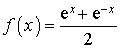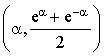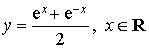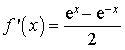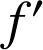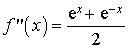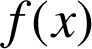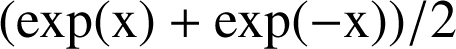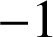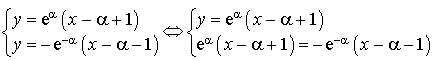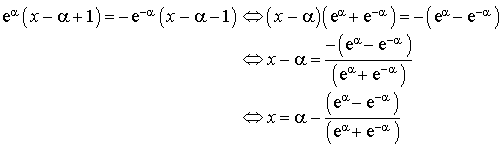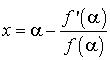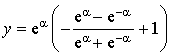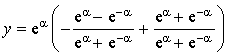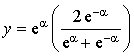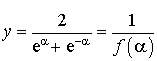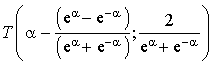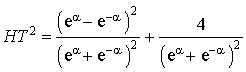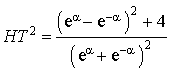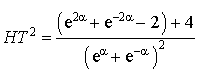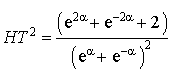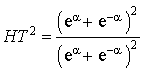Introduction
Durée : 60 minutes
Niveau : moyen
On considère les fonction
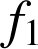 et
et
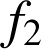 définies pour tout
définies pour tout
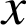 réel par :
réel par :
![]() et
et ![]() .
.
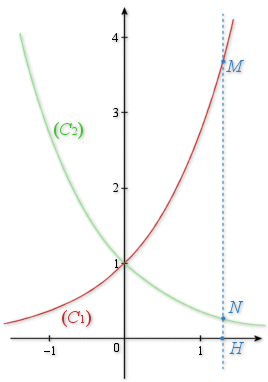
On note
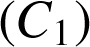 et
et
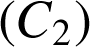 leurs courbes représentatives dans le repère orthonormé
leurs courbes représentatives dans le repère orthonormé ![]() .
.
Soit
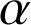 un réel quelconque.
un réel quelconque.
On note
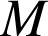 ,
,
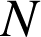 et
et
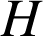 les points d'abscisse
les points d'abscisse
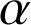 et appartenant à
et appartenant à
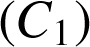 ,
,
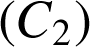 ,
,![]() .
.
2) Déterminer les coordonnées du milieu
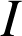 de
de
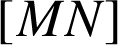 . Quel est le lieu de
. Quel est le lieu de
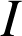 lorsque
lorsque
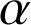 parcourt
parcourt
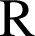 ? Le tracer.
? Le tracer.
3) Déterminer les équations des tangentes
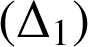 et
et
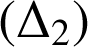 en
en
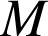 et
et
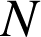 à
à
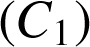 et
et
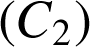 .
.
En utilisant l'outil logiciel, faire une conjecture sur
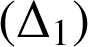 et
et
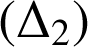 . La démontrer.
. La démontrer.
4) On appelle
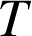 le point d'intersection
le point d'intersection
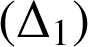 et
et
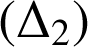 .
.
En utilisant l'outil logiciel, faire une conjecture sur
 . La démontrer.
. La démontrer.