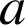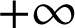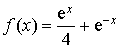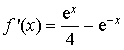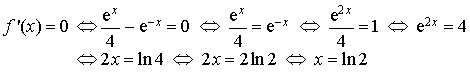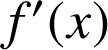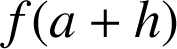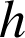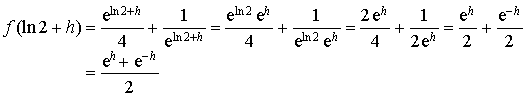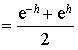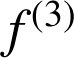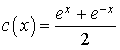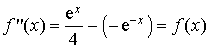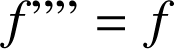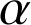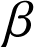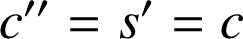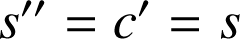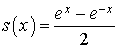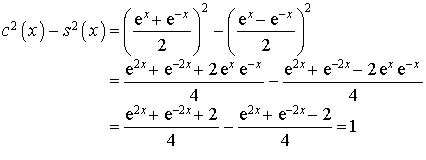Introduction
Durée : 45 minutes
Niveau : moyen
On considère la fonction
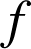définie pour tout
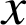réel par 
.
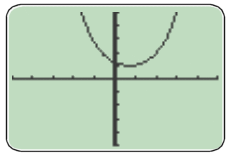
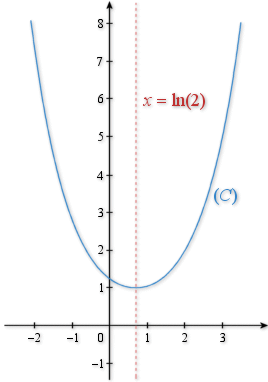
1) Faire afficher la représentation graphique
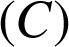de
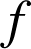sur une calculatrice.
Quel(s) éléments de symétrie de
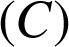peut-on conjecturer ?
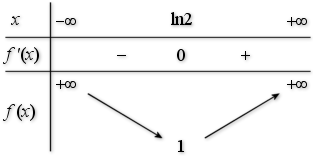
2) Etudier la fonction
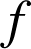et déterminer en particulier son minimum.
4) On considère l'équation différentielle :
.
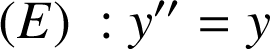a. Montrer que
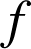est solution de
.
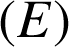b. Montrer que
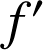est solution de
.
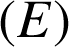c. En déduire que toute les fonctions
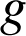de la forme : 
(avec 
) sont solutions de
.
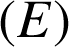d. Soient les fonctions
et
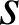définies sur
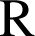par 
et 
.
Montrer que
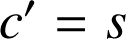et
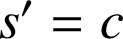, puis que
et
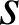sont solution de
.
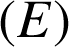Exprimer
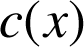et
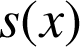en fonction de
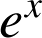et
.
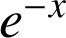Monter que pour tout
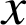réel
.
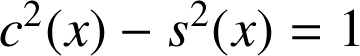