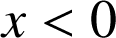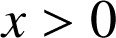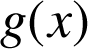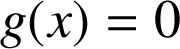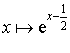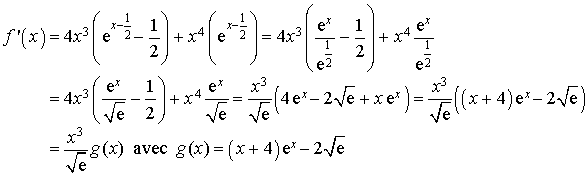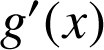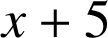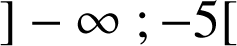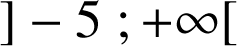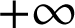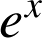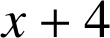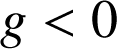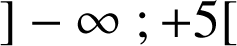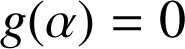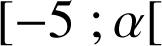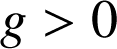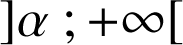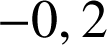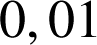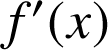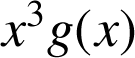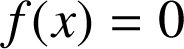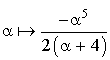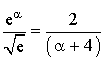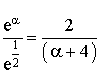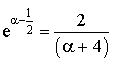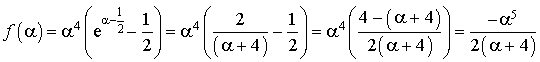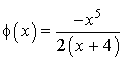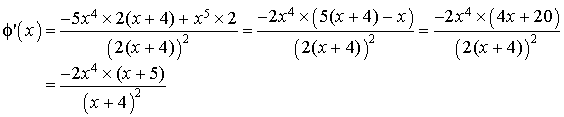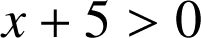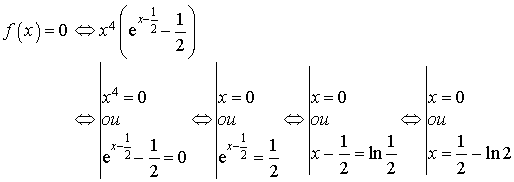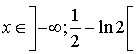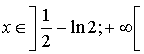Introduction
Durée : 60 minutes
Niveau : moyen
On considère la fonction
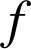définie pour tout
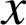réel par 
.
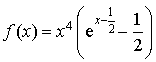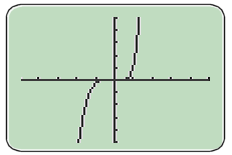
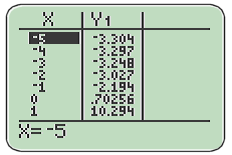
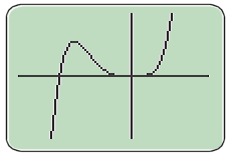
1) Faire afficher la représentation graphique
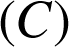de
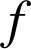sur une calculatrice. Quelles conjectures peut-on faire sur :
a. le sens de variation de
?
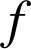b. les points d'intersection de
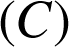avec l'axe des abscisses ?
2) Vérification de la première conjecture
a. Montrer que : 
, 
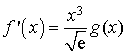, avec 
.
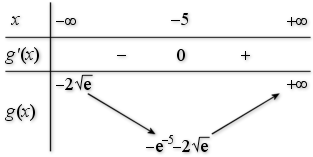
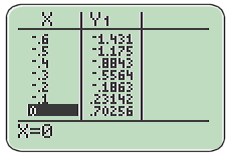
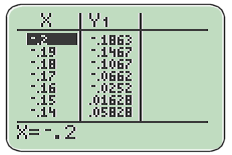
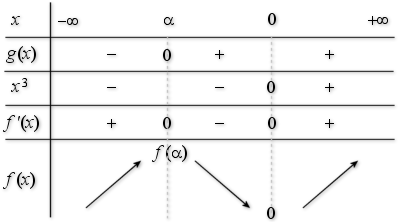
b. Etudier le signe de
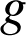(on montrera en particulier que
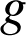s'annule et change de signe en un nombre
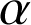dont on donnera un encadrement d'amplitude
).
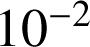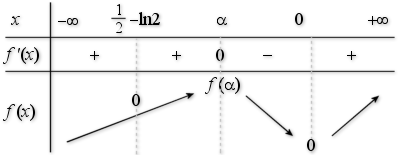
c. En déduire le signe de
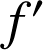et le sens de variation de
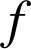. Que dire de la première conjecture ?
3) Vérification de la deuxième conjecture (position de la courbe par rapport à l'axe des abscisses)
a. Montrer que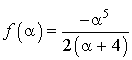 
. Donner un encadrement de
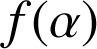d'amplitude 
.
b. Déterminer les abscisses des points d'intersection de
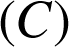avec l'axe des abscisses ; préciser la position de
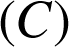par rapport à cet axe.
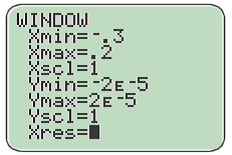
4) Tracer la représentation graphique
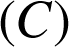de
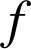sur une calculatrice, en faisant un choix de fenêtre graphique qui permette de visualiser les résultats des questions précédentes.
