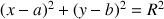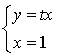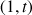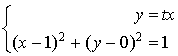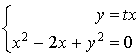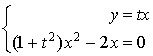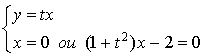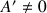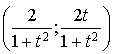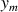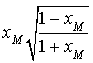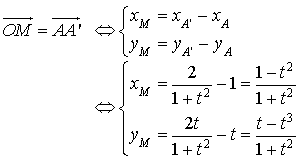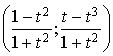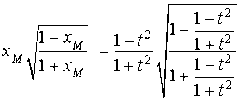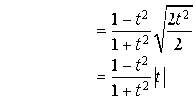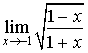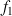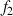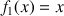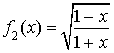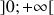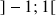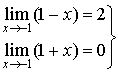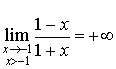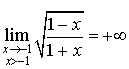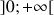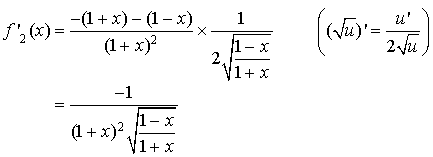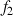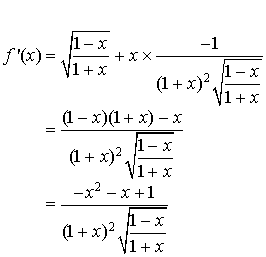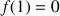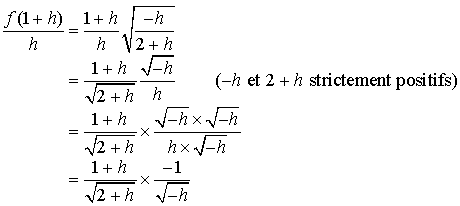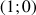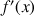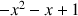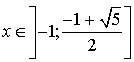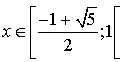Recherche du lieu géométrique d'un point à l'aide d'une fonction
Introduction
Durée : 90 minutes
Niveau : difficile
Recherche du lieu géométrique d'un point à l'aide d'une fonction
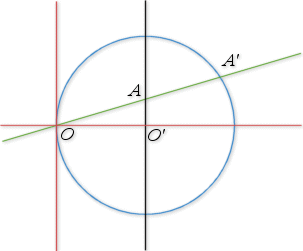
Dans le plan muni d'un repère orthonormal 
(unité de longueur 5 cm), placer le point O' de coordonnées (1,0),
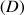la droite d'équation
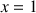et
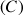le cercle de centre
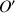et de rayon 1.
1) Pour 
, on note
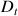la droite d'équation
;
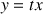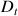coupe la droite
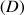en
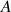et le cercle
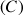en
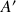et
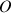; calculer les coordonnées de
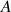et
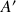en fonction de
.
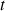2) Soit
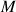le point tel que 
.
a. Déterminer les coordonnées de
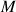en fonction de
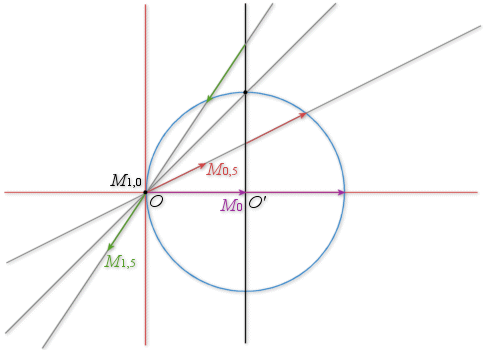
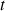; placer les points
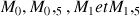correspondant respectivement à
,
,
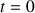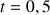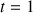et
.
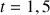b. Montrer que les coordonnées
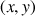de
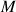vérifient 
et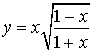 
.
3) Soit
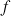la fonction définie sur
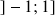par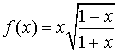 
.
a. Déterminer 
.
b. Déterminer
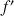fonction dérivée de
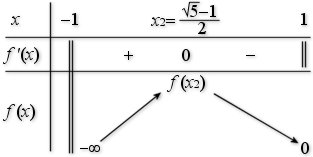
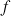; en déduire le tableau de variation de
.
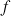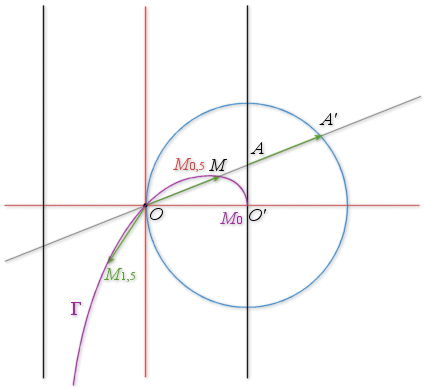
c. Tracer 
la courbe représentative de
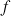; est l'ensemble des points
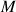définis à la question 2.
