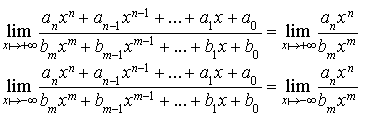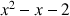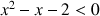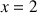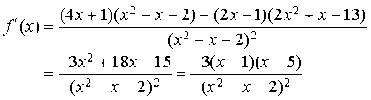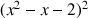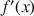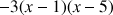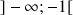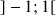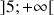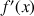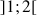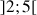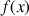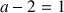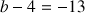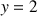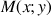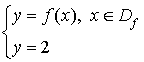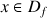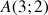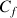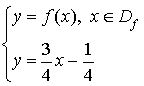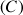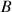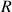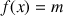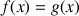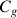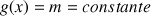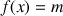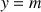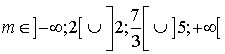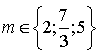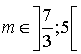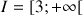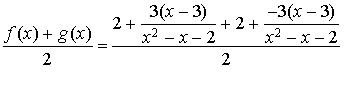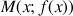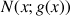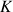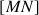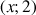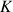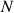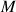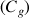Utilisations diverses d'une courbe de fonction rationnelle
Introduction
Durée : 60 minutes
Niveau : moyen
Utilisations diverses d'une courbe de fonction rationnelle
On définit la fonction
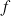par : 
.
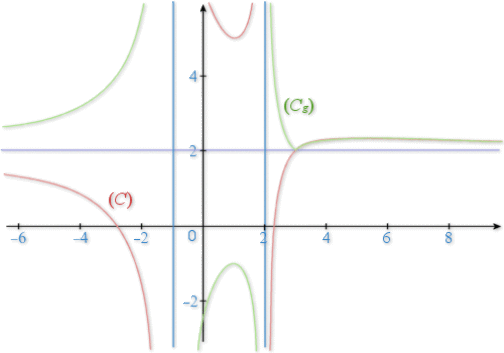
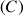est sa représentation graphique dans le repère 
.
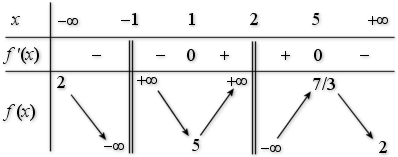
1) Etudier les variations de
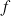sur son ensemble de définition
.
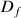2) a. Déterminer les réels a et b tels que :
pour tout
de
, 
.
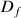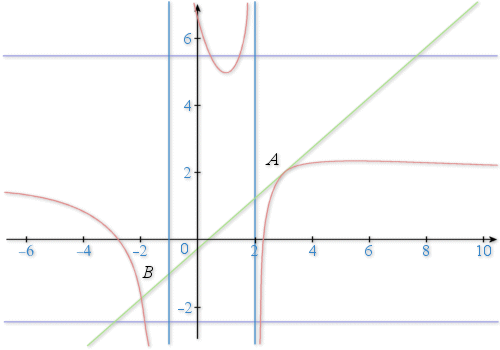
b. En déduire les coordonnées du point
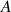où la courbe coupe son asymptote horizontale.
3) a. Donner une équation de la droite
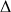tangente à
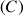au point
.
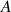b. Déterminer les coordonnées du point
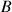où cette tangente recoupe
.
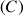4) Tracer dans le repère :
,
,
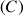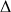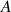et
.
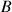5) Soit
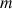un réel quelconque, on note
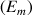l'équation :
En utilisant le graphique précédent, discuter du nombre des solutions de l'équation
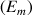suivant les valeurs de
.
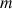6) On définit la fonction
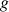par :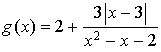 
.
a. Résoudre dans R l'équation
.
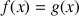b. On appelle
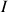l'intervalle solution trouvé à la question a.
Soit 
, calculer 
.
c. Déduire de ce qui précède le tracé de 
dans le repère .
