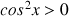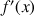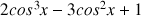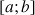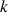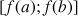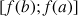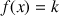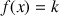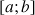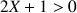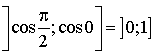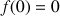Inégalité d'Huygens
Introduction
Durée : 45 minutes
Niveau : moyen
Inégalité d'Huygens
Christian Huygens (1629-1695) : physicien, mathématicien et astronome, on lui doit la réalisation des premières horloges mécaniques.
Démontrer que, pour tout
de 
, 
.
On considère la fonction
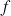définie sur par :
.
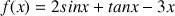1) a. Justifier la dérivabilité de
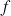sur , puis calculer
.
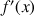b. Montrer que
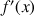a le même signe que
.
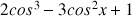2) Soit
.
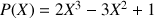a. Vérifier que :
.
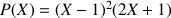b. Déterminer le signe de
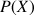pour
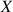élément de
.
3) a. Justifier que la fonction cosinus réalise une bijection de sur
.
b. Déduire des questions précédentes le signe de
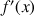sur .
4) Déterminer le signe de
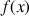sur et conclure sur le problème posé.
