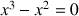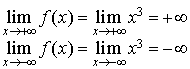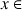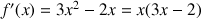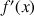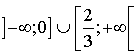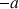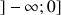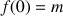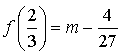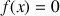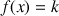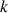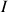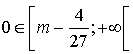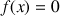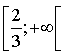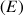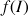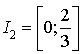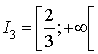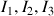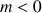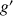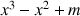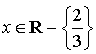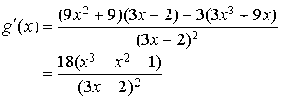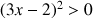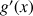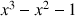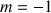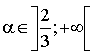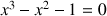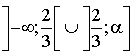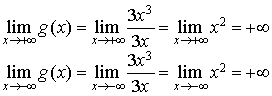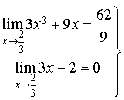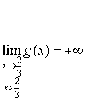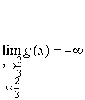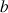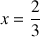Recherche du nombre de solutions d'une équation à l'aide de l'analyse
Introduction
Durée : 50 minutes
Niveau : facile
Recherche du nombre de solutions d'une équation à l'aide de l'analyse
Le but de l'exercice est de déterminer, suivant les valeurs du paramètre m réel, le nombre de solutions de l'équation
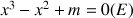et d'utiliser les conclusions trouvées pour établir le sens de variation d'une fonction donnée.
1) Résoudre (
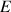) dans le cas particulier où
.
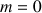2) Pour
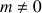, on considère la fonction polynôme
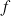définie sur R par
.
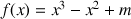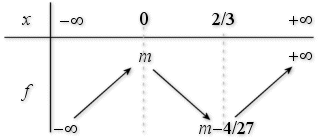
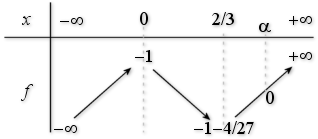
Après avoir étudié les limites de
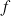en
et
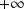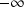et le sens de variation de
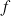, établir le tableau de variation de
.
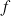3) Justifier que sur R, quel que soit le réel
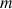, l'équation
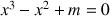admet au moins une solution.
4) Pour quelles valeurs de
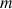l'équation
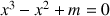admet-elle :
3 solutions (distinctes ou non) ?
une seule solution ?
5) Soit
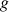la fonction définie sur 
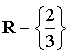par 
.
Justifier qu'il existe un réel 
tel que le sens de variation de
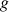soit :
-
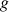est décroissante sur
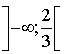et sur 
, -
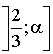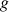est croissante sur
.
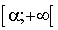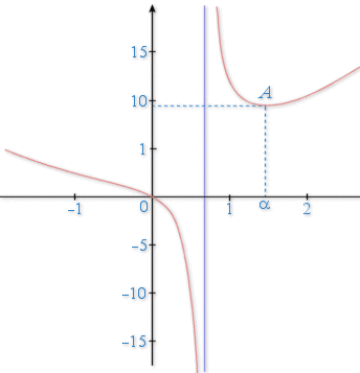
6) Déterminer les limites de
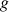en
,
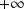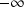et 
.
7) Après avoir justifié que 1,47 est une valeur approchée de
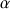par excès à 10-2 près, et en prenant 1,47 pour
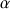, construire la représentation graphique de
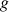dans un repère orthogonal 
.
