limites et ordre
Définition : Comparaison de limites
Soient
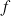 et
et
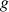 deux fonctions ayant respectivement pour limites
deux fonctions ayant respectivement pour limites
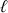 et
et
 (en
(en
 , en
, en
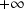 ou en
ou en
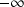 ).
).
Si
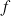 et
et
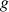 sont dans un certain ordre alors
sont dans un certain ordre alors
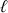 et
et
 sont dans le même ordre.
sont dans le même ordre.
Définition : Limite +∞
Si une fonction
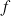 est supérieure ou égale à une fonction
est supérieure ou égale à une fonction
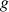 ayant pour limite
ayant pour limite
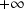 (en
(en
 , en
, en
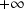 ou en
ou en
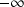 ), alors
), alors
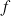 a pour limite (en
a pour limite (en
 , en
, en
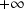 ou en
ou en
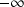 ).
).
Définition : Limite -∞
Si une fonction
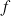 est inférieure ou égale à une fonction
est inférieure ou égale à une fonction
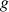 ayant pour limite
ayant pour limite
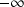 (en
(en
 , en
, en
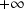 ou en
ou en
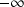 ), alors
), alors
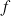 a pour limite
a pour limite
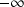 (en
(en
 , en
, en
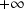 ou en
ou en
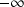 ).
).
Définition : Théorème des « gendarmes »
Si une fonction
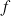 est encadrée par deux fonctions ayant la même limite
est encadrée par deux fonctions ayant la même limite
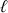 (en
(en
 , en
, en
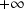 ou en
ou en
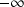 ), alors
), alors
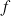 a pour limite
a pour limite
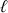 (en
(en
 , en
, en
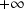 ou en
ou en
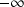 ).
).






