Introduction
Durée : 60 minutes
Niveau : difficile
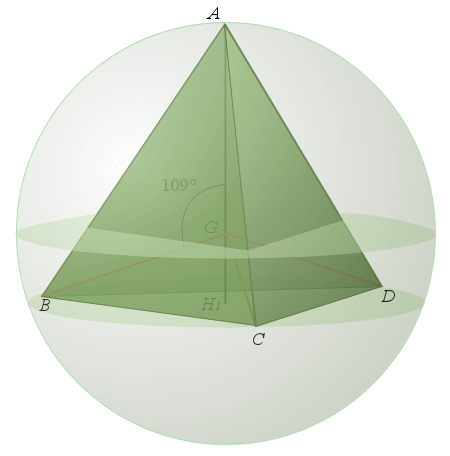
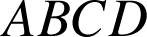 est un tétraèdre régulier de côté
est un tétraèdre régulier de côté
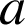 ,
, ![]() le projeté orthogonal de
le projeté orthogonal de
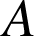 sur le plan
sur le plan ![]() . La droite
. La droite ![]() est une hauteur du tétraèdre
est une hauteur du tétraèdre
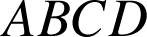 .
.
1)
a. Montrer que le point ![]() est équidistant des points
est équidistant des points
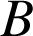 ,
,
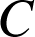 ,
,
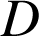 .
.
b. En déduire que ![]() .
.
a. ![]() projeté orthogonal de
projeté orthogonal de
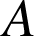 sur
sur ![]() donc
donc ![]() est orthogonale à toute droite de
est orthogonale à toute droite de ![]() .
.
b. Quel rôle joue le point ![]() pour le triangle
pour le triangle
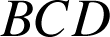 ?
?
a. Les triangles ![]() ,
, ![]() ,
, ![]() sont des triangles rectangle en
sont des triangles rectangle en ![]() ; le théorème de Pythagore permet de calculer les distances
; le théorème de Pythagore permet de calculer les distances ![]() ,
, ![]() ,
, ![]() .
.
Le point ![]() est le projeté orthogonal de
est le projeté orthogonal de
 sur
sur ![]() donc la droite
donc la droite ![]() est perpendiculaire au plan
est perpendiculaire au plan ![]() et donc orthogonale à toute droite de ce plan et en particulier aux droites
et donc orthogonale à toute droite de ce plan et en particulier aux droites ![]() ,
, ![]() ,
, ![]() .
.
En appliquant le théorème de Pythagore dans chacun des triangles rectangles en ![]() ,
, ![]() ,
, ![]() ,
, ![]() :
:
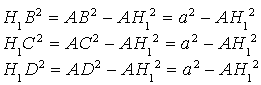
Des distances sont des réels positifs, d'où ![]() .
.
D'après la question a/, ![]() est équidistant des points
est équidistant des points
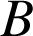 ,
,
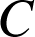 ,
,
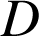 c'est donc le point d'intersection des médiatrices du triangle
c'est donc le point d'intersection des médiatrices du triangle
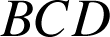 , mais comme le triangle
, mais comme le triangle
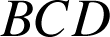 est équilatéral, c'est aussi le centre de gravité ou isobarycentre des points
est équilatéral, c'est aussi le centre de gravité ou isobarycentre des points
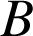 ,
,
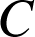 ,
,
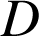 ; il vérifie donc :
; il vérifie donc :
Pour tout point
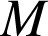 ,
, ![]() et en particulier pour
et en particulier pour ![]() ,
, ![]() .
.
2) Développer le carré scalaire ![]() , le calculer en fonction de
, le calculer en fonction de
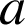 . En déduire
. En déduire ![]() en fonction de
en fonction de
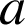 .
.
Si l'on note ![]() ,
, ![]() ,
,![]() les projetés respectifs de
les projetés respectifs de
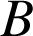 ,
,
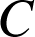 ,
,
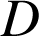 respectivement sur les plans
respectivement sur les plans ![]() ,
, ![]() ,
, ![]() , en déduire les distances
, en déduire les distances ![]() ,
, ![]() ,
, ![]() .
.
Le produit scalaire de 2 vecteurs est défini par ![]() , soit
, soit ![]() .
.
Les propriétés du produit scalaire permettent de développer.
D'après les propriétés du produit scalaire,
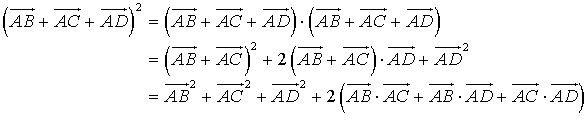
Les triangles
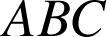 ,
,
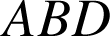 ,
,
 étant des triangles équilatéraux de côté
étant des triangles équilatéraux de côté
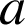 ,
, ![]() et
et ![]() , d'où
, d'où ![]() .
.
D'après la question 1.b/, ![]() , d'où
, d'où ![]() .
.
3) Montrer que l'isobarycentre
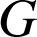 des points
des points
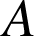 ,
,
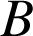 ,
,
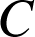 ,
,
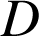 est sur
est sur ![]() et que
et que ![]() . En déduire
. En déduire
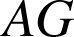 en fonction de
en fonction de
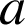 .
.
Justifier que les quatre hauteurs du tétraèdre sont concourantes en
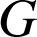 et que
et que
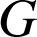 est équidistant des quatre sommets
est équidistant des quatre sommets
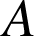 ,
,
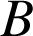 ,
,
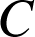 ,
,
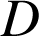 .
.
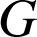 est le barycentre du système
est le barycentre du système ![]() ,
, ![]() ,
, ![]() ,
, ![]() et en utilisant le théorème d'associativité du barycentre,
et en utilisant le théorème d'associativité du barycentre, ![]() peut intervenir.
peut intervenir.
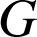 barycentre du système
barycentre du système ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() barycentre du système du système
barycentre du système du système ![]() ,
, ![]() ,
, ![]() donc
donc
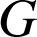 isobarycentre du système
isobarycentre du système ![]() ,
, ![]() (associativité du barycentre).
(associativité du barycentre).
On en déduit donc que ![]() et pour tout point
et pour tout point
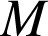 ,
, ![]() , soit pour
, soit pour ![]() ,
, ![]() et
et 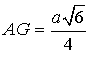 .
.
L'étude faite à l'aide de ![]() peut se faire de la même manière avec
peut se faire de la même manière avec ![]() ,
, ![]() ,
, ![]() et le tétraèdre étant régulier :
et le tétraèdre étant régulier :
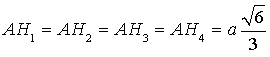
![]()
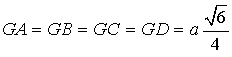
4) En utilisant l'égalité du carré scalaire de ![]() sous la forme
sous la forme ![]() , calculer
, calculer ![]() et en déduire que
et en déduire que ![]() .
.
![]() d'où
d'où ![]() .
.
On en déduit donc 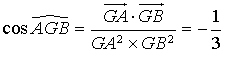 , résultat indépendant de
, résultat indépendant de
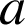 .
.
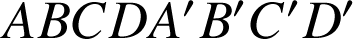 un cube d'arête
un cube d'arête
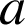 (
(![]() ).
).
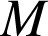 le point du segment
le point du segment ![]() défini par
défini par ![]() avec
avec ![]() .
.
1) Montrer que les triangles
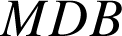 ,
,
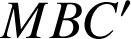 ,
,
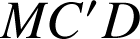 sont isocèles en
sont isocèles en
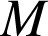 et isométriques.
et isométriques.
Démontrer que les triangles
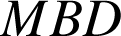 ,
,
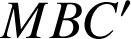 ,
,
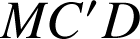 sont isocèles en
sont isocèles en
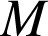 revient à justifier que
revient à justifier que
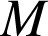 appartient aux plans médiateurs respectivement de
appartient aux plans médiateurs respectivement de ![]() ,
, ![]() ,
, ![]() .
.
La caractéristique de
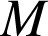 est d'être un point de
est d'être un point de ![]() ; justifier que la droite
; justifier que la droite ![]() est dans les plans médiateurs de
est dans les plans médiateurs de ![]() ,
, ![]() ,
, ![]() permet de conclure que
permet de conclure que ![]() .
.
Observer le comportement de la figure ci-dessous lorsque le point
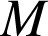 se déplace sur
se déplace sur
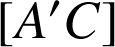 (Macromedia Flash - 11Ko).
(Macromedia Flash - 11Ko).
![]() (diagonale de carré de côté
(diagonale de carré de côté
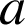 )
)
![]()
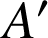 et
et
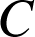 sont équidistants de
sont équidistants de
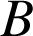 et de
et de
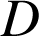 , ils sont donc dans le plan médiateur de
, ils sont donc dans le plan médiateur de ![]() et la droite
et la droite ![]() est contenue dans ce plan médiateur.
est contenue dans ce plan médiateur.
![]() donc
donc
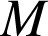 est dans le plan médiateur de
est dans le plan médiateur de ![]() et
et ![]() .
.
Le triangle
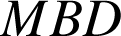 est isocèle en
est isocèle en
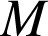 et
et ![]() .
.
A l'aide d'une même démarche,
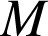 est dans les plans médiateurs de
est dans les plans médiateurs de ![]() et
et ![]() et donc
et donc ![]() ; les triangles
; les triangles
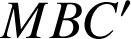 et
et
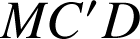 sont isocèles en
sont isocèles en
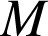 et
et ![]() .
.
Les triangles
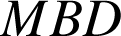 ,
,
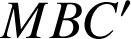 ,
,
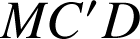 ont les côtés d'extrémités
ont les côtés d'extrémités
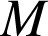 de même longueur et les côtés opposés au sommet
de même longueur et les côtés opposés au sommet
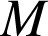 de même longueur, ils sont donc isométriques.
de même longueur, ils sont donc isométriques.
2) On note ![]() :
:
a. Justifier que ![]() .
.
b. En utilisant l'égalité du carré scalaire de ![]() sous la forme
sous la forme ![]() , montrer que
, montrer que ![]() ; en déduire que
; en déduire que ![]() .
.
c. On note
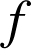 la fonction définie sur
la fonction définie sur ![]() par
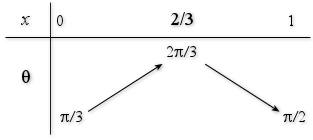
par ![]() ; établir le tableau de variation de
; établir le tableau de variation de
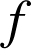 puis en déduire les variations de
puis en déduire les variations de ![]() suivant
suivant
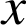 .
.
a.![]()
b. Par hypothèse ![]() ce qui permet d'introduire le réel
ce qui permet d'introduire le réel
 et dans le plan
et dans le plan ![]() ,
,
 est le projeté orthogonal de
est le projeté orthogonal de
 sur
sur ![]() d'où le produit scalaire
d'où le produit scalaire ![]() est égal à
est égal à ![]() .
.
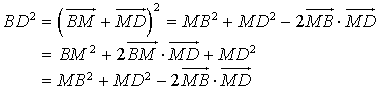
![]() et
et ![]() d'où
d'où ![]() .
.
![]() d'où,
d'où, ![]() .
.
Le triangle
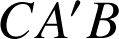 est rectangle en
est rectangle en
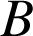 d'où
d'où ![]() .
.
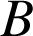 est le projeté orthogonal de
est le projeté orthogonal de
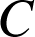 sur
sur ![]() d'où
d'où ![]() .
.
On a donc ![]() .
.
On en déduit donc que ![]() , résultat indépendant de
, résultat indépendant de
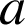 .
.
La fonction
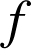 est dérivable sur
est dérivable sur ![]() et
et 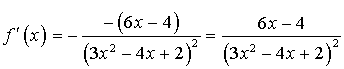 d'où :
d'où :
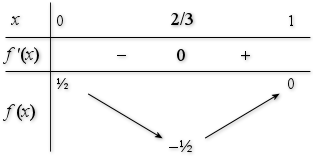
La fonction cosinus est décroissante sur ![]() , les variations de
, les variations de ![]() sont :
sont :
3)
a. Pour quelles valeurs de
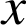 les triangles
les triangles
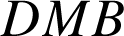 ,
,
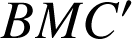 ,
,
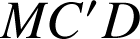 sont-ils rectangles en
sont-ils rectangles en
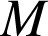 ?
?
b. On se place dans le cas où ![]() . Quel est le rôle du point
. Quel est le rôle du point
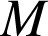 pour le cube ? Que vaut alors
pour le cube ? Que vaut alors ![]() ? Comparer avec le résultat trouvé à la partie (A)4.
? Comparer avec le résultat trouvé à la partie (A)4.
Les triangles
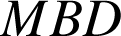 ,
,
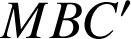 ,
,
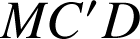 sont rectangles en
sont rectangles en
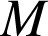 si et seulement si
si et seulement si ![]() donc si et seulement si
donc si et seulement si ![]() .
.
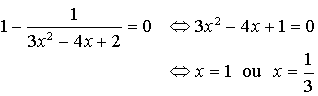
Les triangles
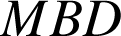 ,
,
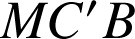 ,
,
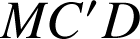 sont rectangles dans deux cas :
sont rectangles dans deux cas :
si
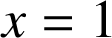 ,
, 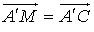 ,
,
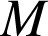 est alors en
est alors en
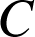 ,
,si
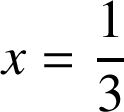 ,
, 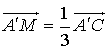 .
.
Si
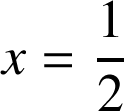 ,
,
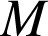 est le milieu de la diagonale
est le milieu de la diagonale ![]() du cube,
du cube,
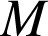 est donc le centre du cube et pour
est donc le centre du cube et pour
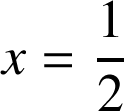 ,
, ![]() , résultat identique à celui trouvé question (A)4.
, résultat identique à celui trouvé question (A)4.






