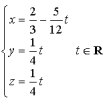Introduction
Durée : 40 minutes
Niveau : moyen
Énoncé de l'exercice
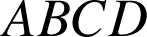 est un tétraèdre,
est un tétraèdre,
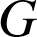 est l'isobarycentre des points
est l'isobarycentre des points
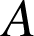 ,
,
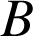 ,
,
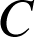 et
et
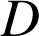 , et
, et
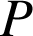 est le point tel que
est le point tel que ![]() .
.
Objectif :
Le but de l'exercice est de justifier l'existence du point
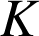 point d'intersection de la droite
point d'intersection de la droite
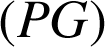 et du plan
et du plan
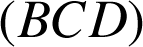 puis de déterminer sa position dans le triangle
puis de déterminer sa position dans le triangle
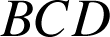 par deux méthodes différentes.
par deux méthodes différentes.
Observer le comportement de la figure ci-dessous lorsque le point A se déplace (Macromedia Flash - 22Ko).
A l'aide des barycentres
1) Montrer qu'il existe un point
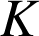 tel que
tel que
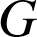 est le barycentre du système
est le barycentre du système ![]() et
et ![]() ; justifier que
; justifier que ![]() et qu'il est à l'intérieur du triangle
et qu'il est à l'intérieur du triangle
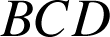 .
.
Les hypothèses sur les points
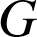 et
et
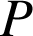 faisant intervenir les barycentres sont :
faisant intervenir les barycentres sont :
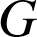 isobarycentre des points
isobarycentre des points
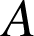 ,
,
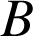 ,
,
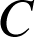 ,
,
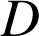 et
et
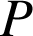 barycentre du système
barycentre du système ![]() ,
, ![]() . Vu la conclusion cherchée, il faut essayer d'introduire
. Vu la conclusion cherchée, il faut essayer d'introduire
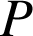 comme barycentre partiel dans un système dont
comme barycentre partiel dans un système dont
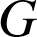 est barycentre.
est barycentre.
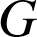 est le barycentre du système
est le barycentre du système ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() est le barycentre partiel de
est le barycentre partiel de ![]() ,
, ![]() .
.
G est le barycentre du système ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
D'après l'associativité du barycentre,
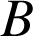 étant le barycentre de
étant le barycentre de ![]() ,
, ![]() et
et
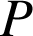 étant le barycentre de
étant le barycentre de ![]() ,
, ![]() (par hypothèse
(par hypothèse ![]() ) :
) :
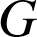 barycentre de
barycentre de ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
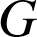 barycentre de
barycentre de ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
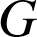 barycentre de
barycentre de ![]() ,
, ![]() où
où
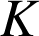 est le barycentre de
est le barycentre de ![]() ,
, ![]() ,
, ![]() .
.
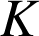 appartient donc à la droite
appartient donc à la droite ![]() et au plan
et au plan ![]() ; de plus les trois coefficients
; de plus les trois coefficients
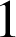 ,
,
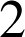 ,
,
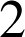 étant strictement positifs, le point
étant strictement positifs, le point
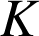 est à l'intérieur du triangle
est à l'intérieur du triangle
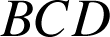 .
.
2) En déduire que la droite ![]() coupe le plan en
coupe le plan en
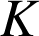 .
.
D'après la question 1), ![]() ; la droite
; la droite ![]() n'étant pas contenue dans le plan
n'étant pas contenue dans le plan ![]() , on peut en déduire que la droite
, on peut en déduire que la droite ![]() coupe le plan
coupe le plan ![]() au point
au point
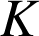 barycentre
barycentre ![]() ,
, ![]() ,
, ![]() .
.
3) Montrer que ![]() et que
et que ![]() .
.
Exprimer
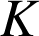 comme barycentre des points
comme barycentre des points
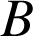 et
et
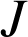 .
.
D'après les résultats précédents,
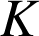 barycentre de
barycentre de ![]() ,
, ![]() ,
, ![]() .
.
Or
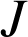 barycentre de
barycentre de ![]() ,
, ![]() donc
donc
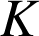 barycentre de
barycentre de ![]() ,
, ![]() .
.
On en déduit que, pour tout
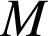 ,
, ![]() et en particulier pour
et en particulier pour ![]() ,
, ![]() .
.
A l'aide de la position relative d'une droite et d'un plan dans l'espace et de la géométrie analytique
1)
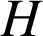 étant l'isobarycentre des points
étant l'isobarycentre des points
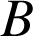 ,
,
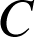 ,
,
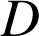 , et
, et
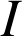 et
et
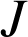 les milieux respectifs des segments
les milieux respectifs des segments
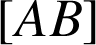 et
et
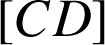 , montrer que
, montrer que ![]() et que
et que
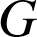 est le milieu de
est le milieu de
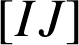 .
.
Si
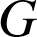 est l' isobarycentre de
est l' isobarycentre de
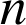 points de l'espace, le cours permet d'écrire une relation vectorielle vérifiée par tout point
points de l'espace, le cours permet d'écrire une relation vectorielle vérifiée par tout point
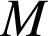 de l'espace puis plus particulièrement pour
de l'espace puis plus particulièrement pour ![]() .
.
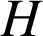 ,
,
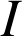 et
et
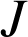 jouent les rôles d'isobarycentre partiel, il est donc possible d'utiliser le théorème d'associativité du barycentre.
jouent les rôles d'isobarycentre partiel, il est donc possible d'utiliser le théorème d'associativité du barycentre.
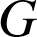 est l'isobarycentre des points
est l'isobarycentre des points
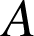 ,
,
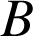 ,
,
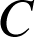 ,
,
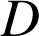 et
et
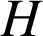 l'isobarycentre des points
l'isobarycentre des points
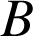 ,
,
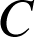 ,
,
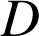 donc pour tout point
donc pour tout point
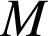 ,
,
![]() et
et ![]()
D'où pour tout point
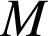 ,
, ![]() (relation que l'on peut obtenir aussi en utilisant le fait que
(relation que l'on peut obtenir aussi en utilisant le fait que
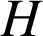 est l'isobarycentre des trois points
est l'isobarycentre des trois points
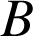 ,
,
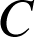 ,
,
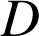 et
et
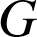 est donc le barycentre des points pondérés
est donc le barycentre des points pondérés ![]() et
et ![]() d'après le théorème de l'associativité du barycentre).
d'après le théorème de l'associativité du barycentre).
Pour ![]() ,
, ![]() et donc
et donc ![]() .
.
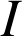 est l'isobarycentre des points
est l'isobarycentre des points
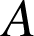 et
et
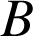 , et
, et
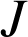 l'isobarycentre des points
l'isobarycentre des points
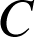 et
et
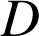 donc :
donc :
D'après le théorème d'associativité du barycentre,
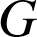 est le barycentre des points pondérés
est le barycentre des points pondérés ![]() et
et ![]() ; les coefficients étant les mêmes,
; les coefficients étant les mêmes,
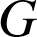 est donc le milieu de
est donc le milieu de
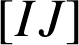 .
.
Pour tout point
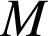 ,
, ![]() et
et ![]() .
.
D'où pour tout point
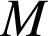 ,
, ![]() , soit pour
, soit pour ![]() ,
, ![]() .
.
2) Montrer que la droite ![]() est incluse dans le plan
est incluse dans le plan ![]() ; en déduire que la droite
; en déduire que la droite ![]() coupe le plan
coupe le plan ![]() en
en
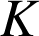 , point de
, point de ![]() .
.
Si deux points distincts de l'espace appartiennent à un plan
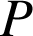 alors la droite déterminée par ces deux points est incluse dans ce plan
alors la droite déterminée par ces deux points est incluse dans ce plan
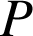 .
.
Quelle est l'intersection des plans ![]() et
et ![]() ?
?
Par hypothèse ![]() , donc
, donc
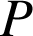 est le barycentre des points pondérés
est le barycentre des points pondérés ![]() et
et ![]() , et donc
, et donc ![]() . Comme la droite
. Comme la droite ![]() est incluse dans le plan
est incluse dans le plan ![]() ,
, ![]() .
.
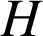 est l'isobarycentre des points
est l'isobarycentre des points
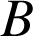 ,
,
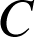 ,
,
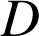 donc
donc
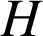 est le centre de gravité du triangle
est le centre de gravité du triangle
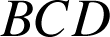 et
et
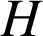 est sur la médiane
est sur la médiane ![]() . Les points
. Les points
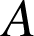 et
et
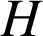 appartiennent au plan
appartiennent au plan ![]() donc la droite
donc la droite ![]() est incluse dans le plan
est incluse dans le plan ![]() .
.
![]() donc
donc ![]() .
.
![]() , donc
, donc ![]() , la droite
, la droite ![]() est donc incluse dans le plan
est donc incluse dans le plan ![]() ;
; ![]() donc
donc ![]() .
.
La droite ![]() est donc dans le plan
est donc dans le plan ![]() et dans ce plan, les droites
et dans ce plan, les droites ![]() et
et ![]() ne sont pas parallèles (
ne sont pas parallèles (![]() et
et ![]() ), donc
), donc ![]() coupe
coupe ![]() (égale à
(égale à ![]() ) en un point
) en un point
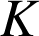 . La droite
. La droite ![]() est la droite d'intersection des plans
est la droite d'intersection des plans ![]() et
et ![]() , la droite
, la droite ![]() coupe le plan
coupe le plan ![]() au point
au point
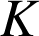 de
de ![]() .
.
3) L'espace étant muni du repère ![]() :
:
a. Calculer les coordonnées des points
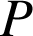 et
et
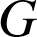 .
.
b. Déterminer une représentation paramétrique de la droite ![]() .
.
c. Montrer que le point
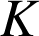 intersection de la droite
intersection de la droite ![]() et du plan
et du plan ![]() vérifie
vérifie ![]() .
.
b. La représentation paramétrique d'une droite ![]() définie par le point
définie par le point
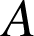 et un vecteur directeur
et un vecteur directeur ![]() est obtenue par la traduction analytique de l'écriture vectorielle,
est obtenue par la traduction analytique de l'écriture vectorielle, ![]() .
.
c. Le point
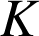 est le point d'intersection de la droite
est le point d'intersection de la droite ![]() et du plan
et du plan ![]() ; quelle est l'abscisse d'un point du plan
; quelle est l'abscisse d'un point du plan ![]() ?
?
Dans le repère ![]() , les points
, les points
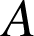 ,
,
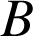 ,
,
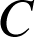 ,
,
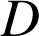 ont respectivement pour coordonnées
ont respectivement pour coordonnées ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Pour tout point
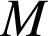 ,
, ![]() et
et ![]() , soit pour
, soit pour ![]() .
.
![]() et
et ![]() d'où
d'où
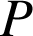 a pour coordonnées
a pour coordonnées 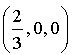 et
et
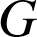 a pour coordonnées
a pour coordonnées 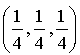 .
.
Une traduction vectorielle du plan ![]() est :
est :
d'où tout point
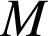 du plan
du plan ![]() a pour abscisse
a pour abscisse
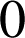 .
.
![]() d'où
d'où ![]() .
.
![]() d'où il existe un réel
d'où il existe un réel
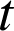 tel que :
tel que :
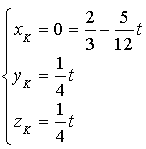
Soit ![]() et
et
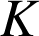 a pour coordonnées
a pour coordonnées 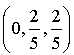 .
.
On en déduit que :