Introduction
Durée : 50 minutes
Niveau : moyen
Énoncé de l'exercice
Le but de l'exercice est de déterminer pour deux droites
 et
et
 de l'espace une droite
de l'espace une droite
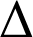 qui est à la fois orthogonale et sécante à
qui est à la fois orthogonale et sécante à
 et
et
 ;
;
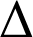 est appelée perpendiculaire commune à
est appelée perpendiculaire commune à
 et
et
 .
.
 et
et
 sont deux droites de l'espace strictement parallèles.
sont deux droites de l'espace strictement parallèles.
Déterminer l'ensemble des perpendiculaires communes.
Deux droites de l'espace strictement parallèles déterminent un plan.
 et
et
 sont strictement parallèles, elles sont donc coplanaires.
sont strictement parallèles, elles sont donc coplanaires.
Dans ce plan :
Par tout point d'une droite, on peut construire une perpendiculaire à cette droite et une seule.
Si deux droites sont parallèles toute perpendiculaire à l'une est perpendiculaire à l'autre.
L'ensemble des perpendiculaires communes à
 et
et
 est donc égal à l'ensemble des perpendiculaires à au moins l'une d'elles.
est donc égal à l'ensemble des perpendiculaires à au moins l'une d'elles.
 et
et
 sont deux droites de l'espace sécantes.
sont deux droites de l'espace sécantes.
Montrer qu'elles possèdent une perpendiculaire commune et une seule.
Deux droites de l'espace sécantes déterminent un plan ; toute droite orthogonale à deux droites sécantes d'un plan est perpendiculaire à ce plan.
 et
et
 sont deux droites sécantes de l'espace, elles sont donc coplanaires.
sont deux droites sécantes de l'espace, elles sont donc coplanaires.
Si
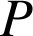 est le plan déterminé par
est le plan déterminé par
 et
et
 , et
, et
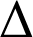 une perpendiculaire commune à
une perpendiculaire commune à
 et
et
 , alors
, alors
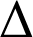 est perpendiculaire au plan
est perpendiculaire au plan
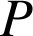 (toute droite orthogonale à deux droites sécantes d'un plan est perpendiculaire à ce plan).
(toute droite orthogonale à deux droites sécantes d'un plan est perpendiculaire à ce plan).
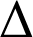 coupe donc le plan
coupe donc le plan
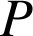 en un seul point et
en un seul point et
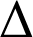 est sécante à
est sécante à
 et
et
 .
.
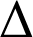 coupe donc
coupe donc
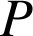 au point d'intersection de
au point d'intersection de
 et
et
 .
.
Par le point d'intersection de
 et
et
 , il passe une perpendiculaire au plan
, il passe une perpendiculaire au plan
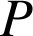 défini par
défini par
 et
et
 et une seule.
et une seule.
Deux droites sécantes de l'espace admettent donc une seule perpendiculaire commune, c'est la perpendiculaire en leur point d'intersection au plan qu'elles déterminent.
 et
et
 sont deux droites de l'espace non coplanaires.
sont deux droites de l'espace non coplanaires.
1) L'espace étant muni d'un repère orthonormal ![]() , les droites
, les droites
 et
et
 ont pour représentation paramétrique respective :
ont pour représentation paramétrique respective :
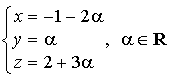
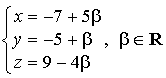
Montrer que
 et
et
 sont non coplanaires.
sont non coplanaires.
Deux droites de l'espace sont coplanaires si elles sont parallèles ou sécantes.
1) D'après leur représentation paramétrique les droites
 et
et
 admettent respectivement pour vecteur directeur
admettent respectivement pour vecteur directeur ![]() et
et ![]() . Ces vecteurs ne sont pas colinéaires (il n'existe pas de réel
. Ces vecteurs ne sont pas colinéaires (il n'existe pas de réel
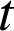 tel que
tel que ![]() ), donc
), donc
 et
et
 ne sont pas parallèles.
ne sont pas parallèles.
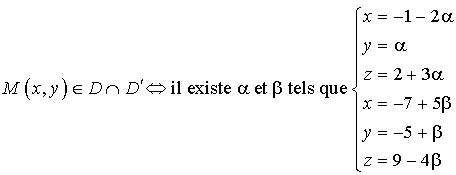
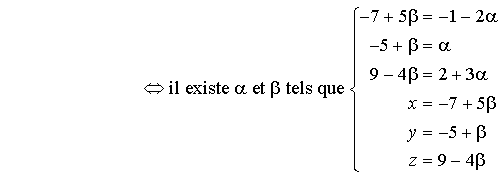
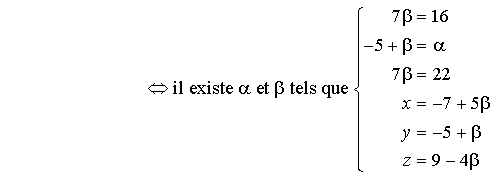
Les équations ![]() et
et ![]() étant incompatibles, ce système n'a pas de solution, les droites
étant incompatibles, ce système n'a pas de solution, les droites
 et
et
 ne sont pas sécantes.
ne sont pas sécantes.
Les droites
 et
et
 ne sont ni sécantes ni parallèles, elles sont non coplanaires.
ne sont ni sécantes ni parallèles, elles sont non coplanaires.
Les droites ![]() et
et ![]() sont non coplanaires si les vecteurs
sont non coplanaires si les vecteurs ![]() ,
, ![]() ,
, ![]() sont non coplanaires.
sont non coplanaires.
![]() ,
, ![]() ,
, ![]() sont coplanaires si et seulement si il existe des réels
sont coplanaires si et seulement si il existe des réels
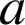 et
et
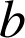 tels que
tels que ![]() .
.
D'après les équations paramétriques de
 et
et
 ,
, ![]() ,
, ![]() , d'où
, d'où ![]() et
et ![]() ,
, ![]() d'où :
d'où :
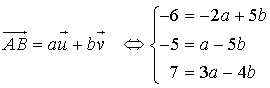
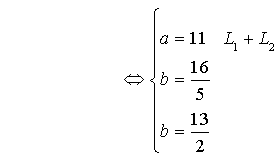
Les deux dernières égalités étant incompatibles, le système n'a pas de solution, les vecteurs ![]() ,
, ![]() ,
, ![]() sont non coplanaires et les droites
sont non coplanaires et les droites
 et
et
 aussi.
aussi.
2) Montrer que la droite ![]() avec
avec ![]() et
et ![]() est une perpendiculaire commune à
est une perpendiculaire commune à
 et
et
 .
.
2) Étude de la position de
 et
et
 :
:
 ayant pour représentation paramétrique
ayant pour représentation paramétrique 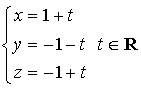 ,
,
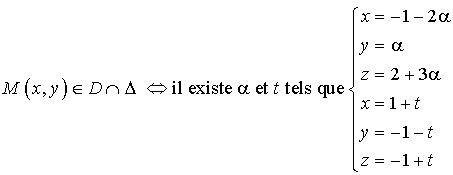
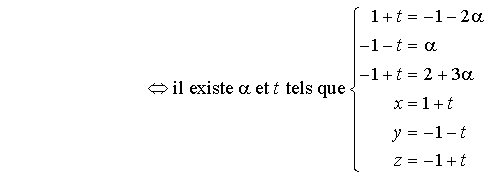
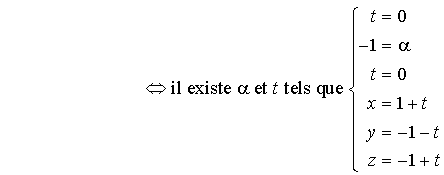
 et
et
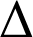 sont donc sécantes en
sont donc sécantes en ![]() ; les vecteurs directeurs de
; les vecteurs directeurs de
 et
et
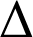 sont orthogonaux (
sont orthogonaux (![]() ), on peut donc en déduire que
), on peut donc en déduire que
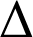 est perpendiculaire à
est perpendiculaire à
 .
.
La même démarche permet de montrer que
 et
et
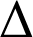 sont sécantes en
sont sécantes en ![]() et que leurs vecteurs directeurs sont orthogonaux ; on peut donc en déduire que
et que leurs vecteurs directeurs sont orthogonaux ; on peut donc en déduire que
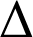 est perpendiculaire à
est perpendiculaire à
 .
.
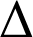 est donc bien une perpendiculaire commune à
est donc bien une perpendiculaire commune à
 et
et
 .
.
3) Justifier que ![]() est la seule perpendiculaire commune à
est la seule perpendiculaire commune à
 et
et
 .
.
Supposer qu'il existe une autre droite
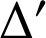 perpendiculaire commune à
perpendiculaire commune à
 et
et
 les coupant respectivement en
les coupant respectivement en
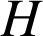 et
et
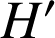 et montrer qu'alors
et montrer qu'alors ![]() .
.
Les points
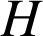 et
et
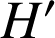 doivent vérifier
doivent vérifier ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
3) Soit
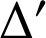 une perpendiculaire commune à
une perpendiculaire commune à
 et
et
 ,
,
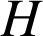 et
et
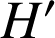 les points d'intersection de
les points d'intersection de
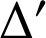 respectivement avec
respectivement avec
 et
et
 .
.
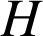 et
et
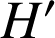 vérifient :
vérifient : ![]() ,
, ![]() (
(![]() ).
).
![]() ,
, ![]() (
(![]() ).
).
![]() et
et ![]() .
.
En écrivant ![]() ,
,
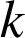 et
et
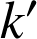 vérifient
vérifient 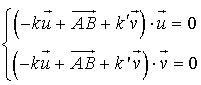 .
.
Or ![]() ,
, ![]() ,
, ![]() , d'où le vecteur
, d'où le vecteur ![]() a pour coordonnées
a pour coordonnées ![]() et
et
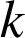 et
et
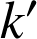 vérifient :
vérifient :
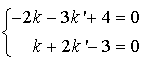
Ce système a une solution unique ; c'est le couple ![]() . Soit
. Soit ![]() et
et ![]() ,
, ![]() et
et ![]() .
.
![]() et
et ![]() ,
,
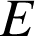 et
et
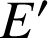 points d'intersection trouvés à la question 2/ donc
points d'intersection trouvés à la question 2/ donc ![]() ; la perpendiculaire commune à
; la perpendiculaire commune à
 et
et
 est unique.
est unique.
REMARQUE :
Deux droites
 et
et
 non coplanaires de l'espace admettent une seule perpendiculaire commune et si
non coplanaires de l'espace admettent une seule perpendiculaire commune et si
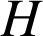 et
et
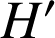 sont les points d'intersection, alors, quels que soient les points
sont les points d'intersection, alors, quels que soient les points
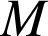 de
de
 et
et
 de
de
 ,
, ![]() . La distance
. La distance
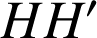 est la distance entre les droites
est la distance entre les droites
 et
et
 .
.
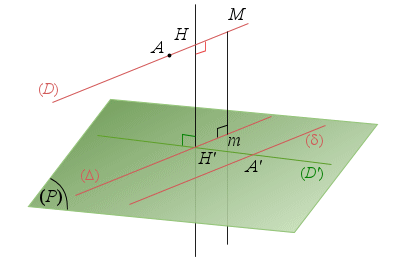
Deux droites ![]() ,
, ![]() non coplanaires et
non coplanaires et
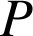 le plan
le plan ![]() , la droite
, la droite
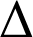 , projection orthogonale de
, projection orthogonale de
 sur
sur
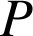 , coupe
, coupe
 en
en
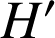 et la perpendiculaire au plan
et la perpendiculaire au plan
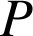 en
en
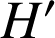 coupe
coupe
 en
en
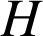 perpendiculairement, et détermine donc la perpendiculaire commune à
perpendiculairement, et détermine donc la perpendiculaire commune à
 et
et
 .
.
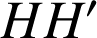 détermine alors la distance entre
détermine alors la distance entre
 et
et
 .
.
L'espace étant muni d'un repère orthonormal ![]() , les droites
, les droites
 et
et
 ont pour repères respectifs
ont pour repères respectifs ![]() ,
, ![]() avec
avec ![]() ,
, ![]() ,
, ![]() ,
, ![]() ; elles sont non coplanaires.
; elles sont non coplanaires.
1) Écrire une représentation paramétrique de
 et
et
 .
.
1) Représentation paramétrique de ![]() :
:
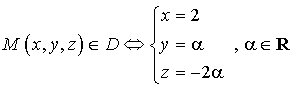
Représentation paramétrique de ![]() :
:
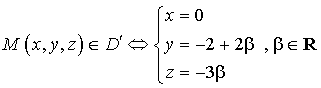
2) Soit deux points ![]() et
et ![]() , déterminer les réels
, déterminer les réels ![]() et
et ![]() tels que la droite
tels que la droite ![]() soit perpendiculaire à
soit perpendiculaire à
 et à
et à
 . En déduire la perpendiculaire commune à
. En déduire la perpendiculaire commune à
 et
et
 .
.
Tout point de
 (respectivement
(respectivement
 ) a des coordonnées qui vérifient le système d'équations paramétriques de
) a des coordonnées qui vérifient le système d'équations paramétriques de
 (respectivement
(respectivement
 ).
).
Deux droites de l'espace sont orthogonales si leurs vecteurs directeurs respectifs sont orthogonaux.
2) ![]() est sur
est sur
 donc il existe un réel
donc il existe un réel ![]() tel que ses coordonnées sont
tel que ses coordonnées sont ![]() et
et ![]() est sur
est sur
 donc il existe un réel
donc il existe un réel ![]() tel que ses coordonnées sont
tel que ses coordonnées sont ![]() .
.
La droite ![]() admet donc pour vecteur directeur
admet donc pour vecteur directeur ![]() .
.
La droite ![]() est donc perpendiculaire en
est donc perpendiculaire en ![]() à
à
 et en
et en ![]() à
à
 si et seulement si il existe un couple
si et seulement si il existe un couple ![]() tel que
tel que 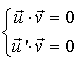 .
.
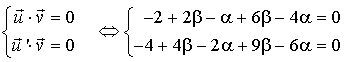
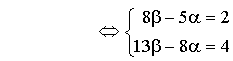
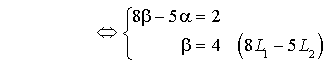

Le système admet un seul couple solution d'où il existe une seule perpendiculaire commune à
 et à
et à
 , c'est la droite
, c'est la droite ![]() avec
avec ![]() de coordonnées
de coordonnées ![]() et
et ![]() de coordonnées
de coordonnées ![]() .
.






