Soit
un tétraèdre régulier (les arêtes sont de même longueur
: 
).
a. Montrer le produit scalaire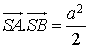 
.
Écrire d'autres produits scalaires égaux à 
.
Montrer que les arêtes opposées sont orthogonales.
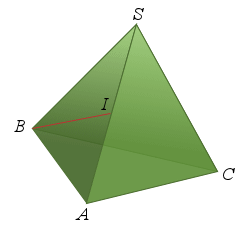
b. Soit
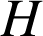le centre de gravité du triangle
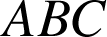. Montrer que la droite
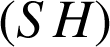est orthogonale au plan
.
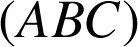a.
Le triangle
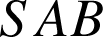est équilatéral. Donc 
et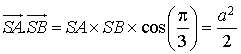 
.
Autre méthode : le milieu
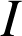de 
est la projection orthogonale de
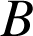sur 
. Donc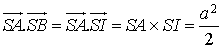 
.
Les autres faces sont également des triangles équilatéraux.
On a de même :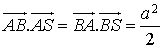 
, mais aussi 
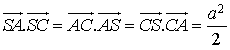, etc.
Par conséquent : 
.
Les vecteurs 
et 
sont orthogonaux, et donc les droites 
et 
sont orthogonales. Il en va de même pour les autres couples d'arêtes opposées : 
et 
ainsi que 
et 
.
b.
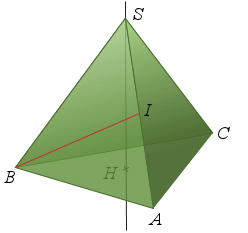
est le centre de gravité de
, donc 
.
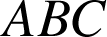Donc 
.
D'après la première question :
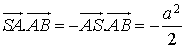
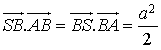
D'où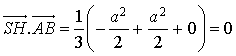 
Donc 
est orthogonale à 
. On démontrait de même que est orthogonale à .
Les droites et ayant des directions distinctes, est orthogonale au plan 
.
Soit
un cube. Que peut on dire de la droite 
et du plan 
?
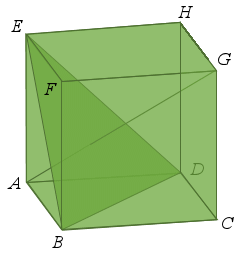
On a 
.
Donc :
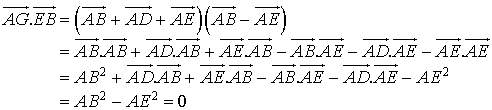
car 
, 
, 
et 
.
On montrerait de même que 
.
Donc la droite est orthogonale aux droites sécantes 
et 
et par conséquent au plan .
L'espace est muni d'un repère orthonormal 
.
Soient 
et 
deux vecteurs de l'espace. Déterminer un vecteur 
non nul et orthogonal à 
et 
?
Le vecteur 
est orthogonal à et si et seulement si :
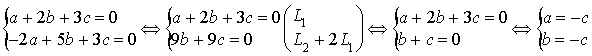
Le système admet comme solution particulière (pour 
) :
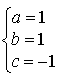
Donc le vecteur 
est orthogonal à et . Il en est de même des vecteurs colinéaires à ce vecteur.
