Définition
Vecteurs orthogonaux
Les vecteurs 
et 
sont orthogonaux si et seulement si leur produit scalaire est nul.
Définition
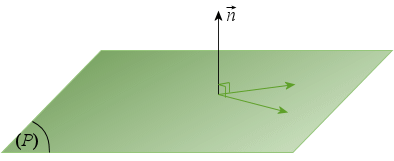
Plan orthogonal à un vecteur. Vecteur normal.
Soit
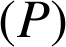un plan et 
un vecteur non nul.
Le plan
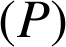est orthogonal à si et seulement si est orthogonal à deux vecteurs non colinéaires de
.
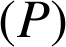est aussi appelé vecteur normal de
.
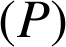