Implicitement, lorsque des coordonnées sont utilisées, l'espace est muni d'un repère orthonormal .

Soit 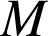un point et 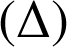une droite de l'espace. On appelle projection orthogonale de 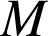sur 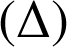le point 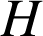, intersection de 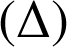et du plan orthogonal à 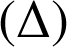et contenant .

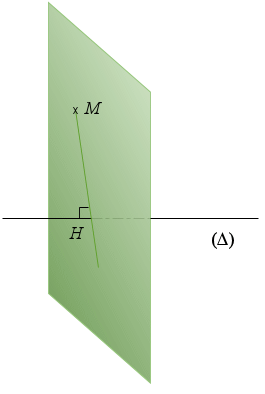
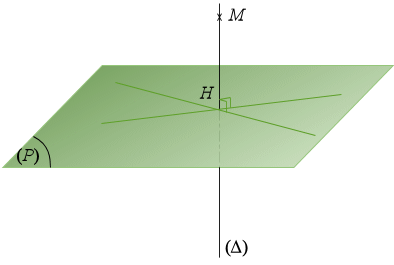
Soit 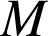un point et 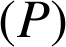un plan de l'espace. On appelle projection orthogonale de 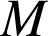sur 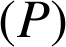le point 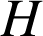, intersection de 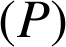et de la droite orthogonale à 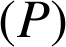passant par .
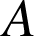