On considère deux vecteurs et .

Les définitions suivantes du produit scalaire de ces deux vecteurs sont équivalentes :

• Il existe au moins un plan 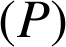contenant les points 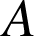, 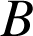et .

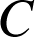  Le produit scalaire des vecteurs 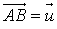et 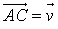est le produit scalaire de ces vecteurs dans le plan 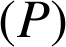et cette définition est indépendante du plan 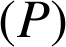choisi.

• .

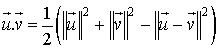• Si 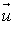a pour coordonnées 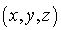et 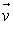a pour coordonnées , .

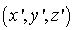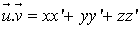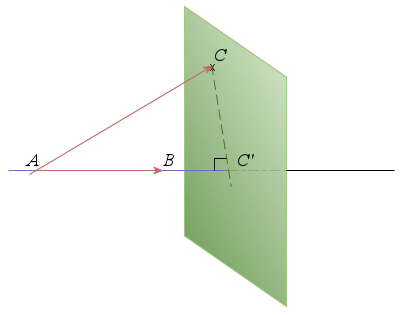
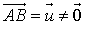• Si : si est la projection orthogonale de 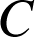sur , .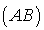

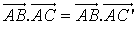  Remarque : si ,

  

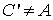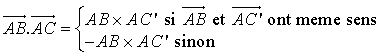
• Si , .

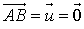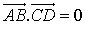Remarque : Si et sont deux vecteurs non nuls, (comme dans le plan).