L'espace est muni d'un repère orthonormal 
. On donne les points 
, 
, 
.
Calculer le produit scalaire 
et en déduire une valeur approchée à
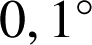près de la mesure en degrés de l'angle 
.
Calculer de même une valeur approchée de la mesure en degrés de l'angle 
.
Les vecteurs 
et 
ont pour coordonnées 
et 
.
De la formule 
,
on déduit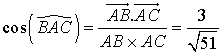 
.
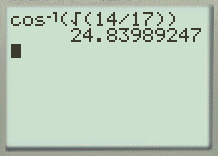
La calculatrice donne alors :
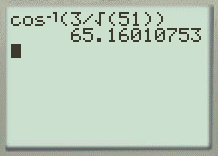
On procède de même pour le deuxième angle :
Les vecteurs 
et 
ont pour coordonnées 
et 
.
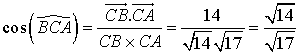
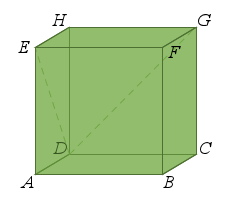
est un cube. Calculer l'angle géométrique 
.
Soit
la longueur de l'arête du cube. Calculons 
.
(
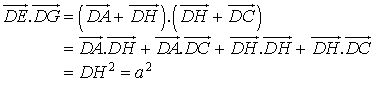
car 
et de même 
et 
)
D'autre part, 
.
Donc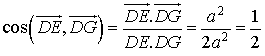 
.
L'angle 
est donc 
.
Remarque : on peut aussi effectuer les calculs dans le repère orthonormal 
.
est un pavé droit. 
et 
.
Calculer à
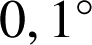près l'angle géométrique 
.
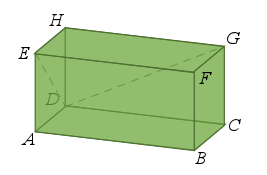
Calculons .
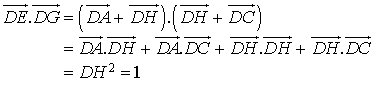
( car et de même et )
D'autre part 
et 
.
Donc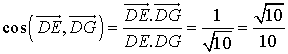 
.
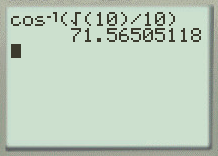
L'angle a donc
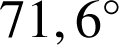pour valeur approchée à
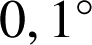près.
