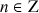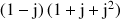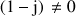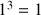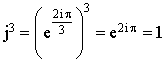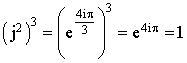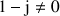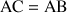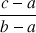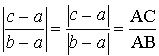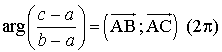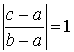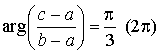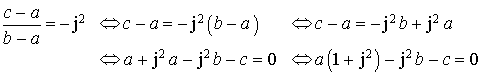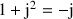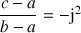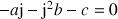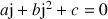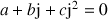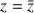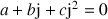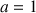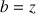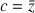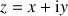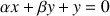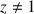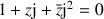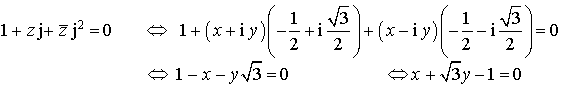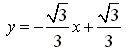Exercice : Etude du nombre complexe j et conséquence géométrique
Introduction
Prérequis :
Calculs dans C : forme algébrique, forme exponentielle, arguments.
Équation de droite.
Durée : 75 minutes
Niveau : difficile
Le plan complexe
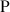est rapporté à un repère orthonormal direct 
(unité graphique : 2 cm).
On dit qu'un triangle équilatéral
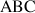est direct si et seulement si 
.
On pose 
.
1)
a. Vérifier que
,
,
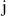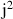sont solutions de l'équation :
.
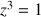b. Calculer
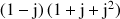; en déduire que
.
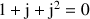c. Vérifier que : 
.
2) Dans le plan complexe, on considère trois points
,
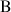et
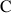deux à deux distincts, d'affixes respectives
,
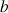et
.
a. Démontrer que le triangle
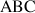est équilatéral direct si et seulement si : 
.
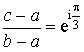b. En utilisant les résultats des questions précédentes, montrer que le triangle
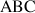est équilatéral direct si et seulement si : 
.
3) A tout nombre complexe
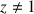, on associe les points
,
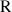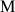et
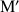d'affixes respectives
,
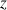et
.
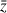a. Pour quelles valeurs de
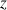les points
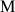et
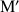sont-ils distincts ?
b. En supposant que la condition précédente est réalisée, montrer que l'ensemble
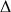des points
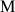d'affixe
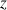tels que le triangle
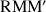soit équilatéral direct est une droite privée d'un point.
