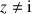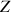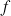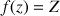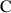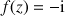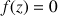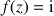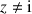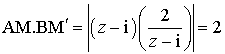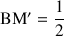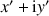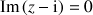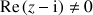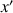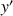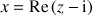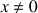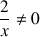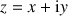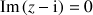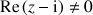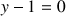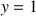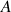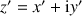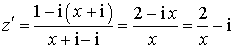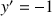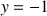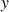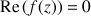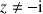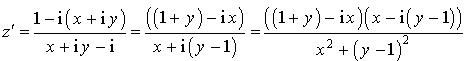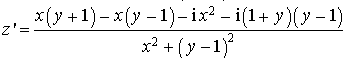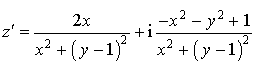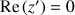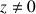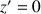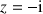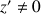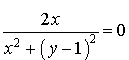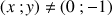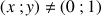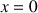Exercice : Fonction complexe, recherche d'ensembles
Introduction
Prérequis :
Calculs dans C : forme algébrique , modules.
Notion d'antécédents.
Recherche de lieux géométriques (droites et cercle).
Durée : 75 minutes
Niveau : difficile
Le plan complexe
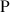est rapporté à un repère orthonormal direct 
(unité graphique : 4 cm).
Soit
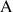le point d'affixe
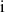et
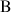le point d'affixe
.
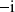Soit
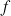la fonction définie sur 
par 
.
2)
a. Démontrer que
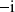n'a pas d'antécédent par
.
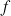b. Déterminer les antécédents de
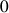et de
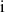par
.
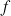3) A tout point
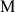différent de
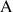, d'affixe
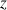, on associe le point
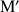d'affixe
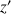tel que
.
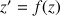a. Démontrer que pour tout point
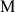différent de
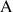, le produit des longueurs
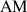et
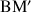est égal à
(
).
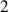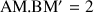b. Démontrer que lorsque
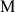décrit le cercle
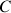de centre
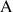et de rayon
,
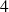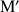se déplace sur un cercle
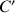dont on précisera le centre et le rayon.
4)
a. Déterminer l'ensemble
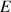des points
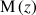tels que
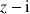soit un nombre réel non nul.
b. Démontrer que lorsque
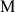décrit
,
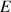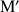se déplace sur une droite
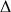que l'on précisera.
c. Lorsque
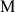décrit
,
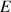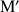décrit-il toute la droite
?
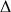5) Déterminer l'ensemble des points
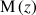tels que
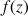soit un imaginaire pur non nul.
