Les propositions suivantes sont-elles vraies ou fausses ? (justifier)
1) Si l'entier naturel
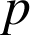est premier, alors
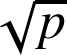n'est pas un entier.
1) Utilisons un raisonnement par l'absurde et supposons que
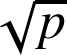soit un entier
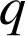, alors 
.
De plus comme
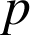est premier,
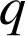est différent de
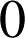et
.
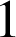Par conséquent
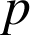possède au moins trois diviseurs distincts :
,
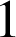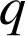et
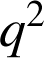. Et ceci contredit le fait que
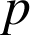soit premier.
Donc
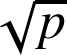n'est pas un entier. La proposition est donc vraie.
2) Pour un entier naturel,
;
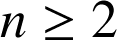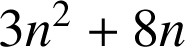n'est jamais premier.
2) 
. Comme
, 
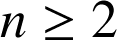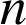et,
et
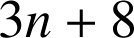sont deux diviseurs propres de
.
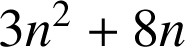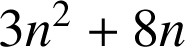n'est pas premier.
Soit
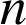un entier (
).
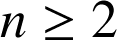On pose 
(
=factorielle
)
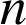1) Soit
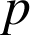un nombre premier divisant N
Montrer que
.
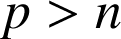1) Utilisons un raisonnement par l'absurde et supposons que
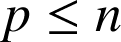. Alors 
Comme
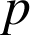est un entier premier,
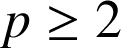donc
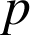ne divise pas
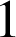et
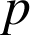ne divise pas .
Et ceci contredit l'hypothèse «
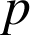divise », donc
.
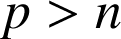2) Que peut-on en conclure sur l'ensemble 
des nombres premiers ?
2) Pour tout entier
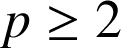, admet un diviseur premier
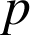donc d'après la question 1,
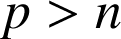. On peut toujours déterminer un entier premier supérieur à n'importe quel entier supérieur ou égal à
.
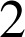Cela signifie que l'ensemble des nombres premiers est infini.
