Suites récurrentes
Soit
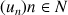une suite de nombres réels définie par son premier terme
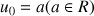et pour tout
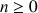une relation de récurrence de la forme
où f est une fonction réelle d'une variable réelle.
Par exemple, on peut considérer la suite de réels définie par
on a ici a = 1 et
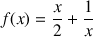
Calcul du terme d'indice n
On veut calculer le terme un lorsqu'est donné l'indice n.
Algorithme 5.3 Calcul du terme d'indice n d'une suite récurrente
Entrée : n un nombre réel, a un réel et f :
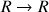une fonction.
Sortie : le terme un de la suite
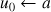
pour i variant de 1 à n faire
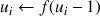
fin pour
renvoyer
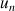
Pour réaliser cet algorithme en Python, il suffit d'utiliser une seule variable pour mémoriser les valeurs successives des termes de la suite.
>>> for i in range (0,n):
... u=f(u)
...
Calcul et affichage des termes d'indice 0 à n
On veut afficher la valeur de tous les termes de la suite (un) dont les indices sont compris entre 0 et n.
Il suffit de calculer successivement chaque terme de la suite et afficher immédiatement sa valeur.
>>> for i in range (0,n):
... print(u)
... u=f(u)
...
Calcul du premier terme satisfaisant une condition
On peut aussi vouloir chercher le premier terme de la suite qui satisfait une condition donnée.
Cette condition peut porter sur le dernier terme calculé, ou bien sur plusieurs termes déjà calculés.
Algorithme 5.4 Calcul du premier terme satisfaisant une condition
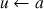
tant que u ne satisfait pas la condition voulue faire
on calcule le terme suivant
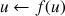
fin tant que
renvoyer u
Remarque :
Si aucun terme de la suite ne satisfait la condition donnée, la boucle est infinie (le programme ne s'arrête pas). Aussi avant de concevoir de tels programmes est-il important de s'assurer qu'au moins un terme de la suite vérifie la condition.
Autres suites récurrentes
Suites récurrentes d'ordre plus élevé
ordre 2 : la suite de Fibonacci définie par ses deux premiers termes et une relation de récurrence
d'ordre 2
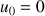
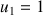
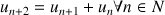
Facile à programmer.
ordre total : la suite des nombres de Catalan définie par son premier terme et une relation de récurrence s'appuyant sur tous les termes qui précèdent
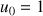
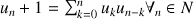
Difficile à programmer sans tableaux ...
