La boucle Pour
On peut calculer la somme des entiers de 1 à n à l'aide d'une structure itérative tant que et de deux variables, i pour énumérer les entiers successifs de 1 à n, et S pour les cumuler.
Algorithme 5.1 Calcul de la somme des n premiers nombres entiers.
Entrée : n un entier positif ou nul
Sortie :
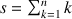
initialiser S à 0
initialiser i à 1
{on a bien
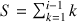 }
}
tant que
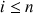 faire
faire
ajouter i à S
incrémenter i
{notons qu'on a toujours
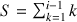 }
}
fin tant que
{la même égalité est satisfaite avec
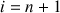 }
}
renvoyer s
Compte tenu de la condition, il est possible de dire avant l'exécution de cet algorithme que la séquence d'instructions contenue dans la boucle tant que sera effectuée n fois.
De manière plus générale, si un algorithme s'écrit de cette façon
initialiser i à a
tant que
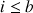 faire
faire
séquence d'instructions ne modifiant pas i
incrémenter i
fin tant que
et que la séquence d'instructions précédant l'incrémentation de la variable i ne modifie pas la valeur de cette variable, alors le nombre de fois que la séquence d'instructions sera exécutée est
égal à
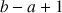 .
.
De telles itérations dont le nombre d'étapes est déterminée par une variable qui parcourt l'ensemble des valeurs comprises entre deux bornes est appelée une boucle pour, et la variable i
est appelée indice de la boucle.
On peut réécrire le calcul de la somme des entiers compris entre 1 et n en utilisant une boucle pour.
Algorithme 5.2 Calcul de la somme des n premiers nombres entiers avec une boucle pour
Entrée : n un entier positif ou nul
Sortie :
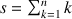
initialiser S à 0
pour i variant de 1 à n faire
ajouter i à S
{on a
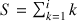 }
}
fin pour
renvoyer s





