Ecoulement en charge
Hypothèses
Fluide newtonien, incompressible, les forces de pesanteur n'interviennent pas dans le problème
On écrit les équations de Navier Stockes :
μ est la viscosité dynamique et ρ la masse volumique
On ajoute l'équation de continuité (conservation de la masse)
Projection des équations dans un repère
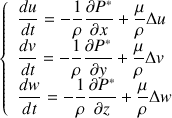
u,v,w sont les composantes de la vitesse dans le repère considéré
Ecriture des variables réduites
Objectif : écrire une équation sans dimension.
On appelle D une dimension caractéristique de l'écoulement ( largeur d'un obstacle, diamètre d'une canalisation, largeur d'un canal).
On pose :

Soit V une vitesse caractéristique de l'écoulement (vitesse non perturbée loin de l'obstacle...).

Les temps sont ramenés à :

De même pour la pression :

On peut donc maintenant écrire une équation sans dimension, celle ci fera apparaître les nombres sans dimension pour les conditions de similitudes.
Écriture des des relations entre grandeurs intervenant dans l'équation de Navier Stokes
Cette équation est sans dimension. Elle est valable pour le prototype et pour la maquette.
Le nombre de Reynolds caractérise donc les équations générales de l'écoulement.





