Equation locale
Forme générale
Sur chaque élément de volume de fluide, on définit :
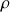la masse volumique.
la densité volumique de force.
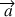l'accélération par rapport au référentiel galiléen O, x, y, z.
Ecriture de l'équation intégrale
Ecrivons la relation fondamentale de la dynamique relativement au référentiel Galiléen O,x ,y,z :
En utilisant la formule du gradient :
On obtient :
La relation précédente est vraie quelque soit l'élément de volume choisi, on peut donc écrire :
Cette équation représente la forme locale de l'équation d'Euler (vraie en chaque point du fluide).
A partir du bilan des forces appliquées au fluide et des caractéristiques cinématiques de l'écoulement, c'est cette équation qui nous servira pour l'étude des écoulements.
Autres expressions de l'équation d'Euler
Dans l'équation précédente, l'accélération du fluide s'écrit (cinématique des fluides) :
Dans cette expression :
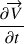est l'accélération locale (non permanence de l'écoulement).
est l'accélération convective (non uniformité de l'écoulement).
