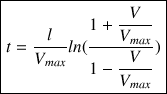Etablissement de l'écoulement dans une conduite
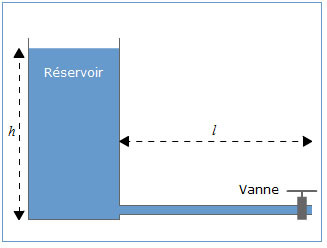
On considère une conduite horizontale, de section constante, de longueur l, alimentée par un réservoir de grandes dimensions où le niveau est maintenu constant. A l'extrémité de la conduite, une vanne permet de réguler le débit. A l'instant t = 0, la vanne est fermée et on l'ouvre brutalement.
Question
Etablir la relation entre le temps d'établissement de l'écoulement et la vitesse maximale du fluide.
1 - Utilisez la relation de Bernoulli en mouvement non permanent entre un point de la surface libre et un point à la sortie du tuyau.
2 -
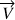ne dépend que du temps, on a donc la formule suivante :
Etablir la relation entre le temps d'établissement de l'écoulement et la vitesse maximale du fluide.
En un point à la distance x de O la relation de Bernouilli en régime non permanent s'écrit :
La section du tuyau est constante donc V et
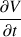ont la même valeur le long du tuyau. En
, la relation précédente s'écrit donc :
Comme V ne dépend que du temps, on peut écrire
. L'équation devient donc :
En intégrant, on obtient :
L'intégration précédente fait apparaître une constante, mais celle-ci est nulle car la vitesse est nulle à t=0.
Lorsque
;
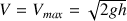, on se trouve dans le cas de l'écoulement permanent (formule de Torricelli), on peut donc écrire :
