Le volley-ball
Un joueur de volley-ball est au service d'un ballon qu'il lance avec une vitesse initiale
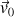faisant un angle
avec le plan horizontal (voir schéma ci-dessous). Le ballon est frappé avec la main à la hauteur
du sol et à la distance
du filet. La hauteur du filet est
, et la limite du camp adverse est à la distance
du filet. Pour que le service soit bon, le ballon doit passer par-dessus le filet et doit toucher le sol dans le camp adverse entre le filet et la limite du camp adverse.
Pour simplifier, on considère que le mouvement se fait dans un plan vertical orthogonal au filet et contenant
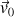. L'étude du mouvement se fera dans le repère
, où l'axe
est horizontal et l'axe
est vertical dirigé vers le haut. Le centre d'inertie G du ballon est initialement au point P(
). Les frottements de l'air sont négligés et on prendra
.
Question
Caractériser le vecteur accélération
du centre d'inertie G du ballon.
Le système étudié est le ballon de volley-ball.
Le référentiel choisi est terrestre (supposé galiléen).
Les forces extérieures qui agissent sur le système sont :
- le poids
- les frottements de l'air, mais que l'on néglige (dit dans l'énoncé).
On applique la deuxième loi de Newton :
Le vecteur accélération
du centre d'inertie G du ballon est donc :
Question
Déterminer les composantes de l'équation horaire du vecteur vitesse
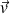du ballon.
Le vecteur accélération correspond à la variation du vecteur vitesse :
Pour obtenir les coordonnées du vecteur vitesse
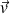, on part des coordonnées du vecteur accélération :
On intègre les équations différentielles pour trouver les coordonnées du vecteur vitesse :
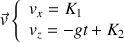
On doit évaluer les constantes
et
. Les coordonnées du vecteur vitesse doivent être exactes même pour
. D'après la relation ci-dessus, on a :
Or d'après l'énoncé, le ballon est lancé avec une vitesse initiale
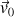faisant un angle
avec l'horizontale, soit :
On identifie alors :
Ce qui donne pour les coordonnées du vecteur vitesse :
ou :
Question
Déterminer les composantes de l'équation horaire du vecteur position
du ballon.
Le vecteur vitesse correspond à la variation du vecteur position :
Pour obtenir les coordonnées du vecteur position
, on part des coordonnées du vecteur vitesse :
On intègre les équations différentielles pour trouver les coordonnées du vecteur position :
On doit évaluer les constantes
et
. Les coordonnées du vecteur position doivent être exactes même pour
. D'après la relation ci-dessus, on a :
Or d'après l'énoncé, le ballon est lancé d'un point P de coordonnées
, soit :
On identifie alors :
Ce qui donne pour les coordonnées du vecteur position :
ou :
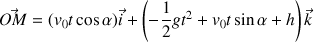
Question
Mouvement de G.
a) Déterminer l'équation de la trajectoire du ballon.
b) Quelle est la trajectoire du ballon ?
c) Comment appelle-t-on ce type de mouvement ? Pourquoi ?
a) Pour écrire l'équation de la trajectoire, il faut éliminer le temps entre les composantes du vecteur position. On a :
On utilise la composante
pour exprimer le temps sous la forme :
On peut alors remplacer le terme temporel de la composante
par celui que l'on vient d'écrire :
On obtient une expression qui ne dépend plus du temps.
b)Cette expression est de la forme
, c'est donc l'équation d'une parabole. La trajectoire du ballon est parabolique.
c) Ce type de mouvement est appelé mouvement de chute libre, car la seule force en jeu dans
le mouvement est le poids.
Question
La vitesse initiale
doit être comprise entre deux valeurs pour que le service soit bon : une valeur minimale
telle que le ballon arrive au sol en passant juste au dessus du filet (soit pour
), et une valeur maximale
telle que le ballon arrive au sol à la limite du camp adverse (soit pour
).
a) Donner la relation littérale de
. Calculer numériquement
.
b) Donner la relation littérale de
. Calculer numériquement
.
c) Donner l'encadrement de vitesse de
.
a) Si le ballon atteint la vitesse
, il doit passer exactement par la position
, soit, en reportant cette condition dans l'équation de la trajectoire :
Ce qui donne :
b) Si le ballon atteint la vitesse
, il doit passer exactement par la position
, soit, en reportant cette condition dans l'équation de la trajectoire :
Ce qui donne :
c) Pour que le ballon tombe dans les limites du terrain après service, il faut que la vitesse initiale soit dans l'encadrement :
Question
Déterminer
la distance depuis le filet jusqu'au point de chute du ballon si la vitesse initiale du ballon est de
.
Maintenant, on considère que la vitesse initiale est
. Le point de chute du ballon est donné par la condition
, soit, en reportant cette condition dans l'équation de la trajectoire :
On obtient une équation polynomiale du second degré de la forme :
On résout cette équation en calculant le discriminant :
Et les deux racines :
Seule la solution
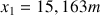est valable. Mais on cherche
, la distance depuis le filet jusqu'au au point de chute du ballon, c'est-à-dire :
