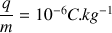Déviation d'une particule chargée par action de deux champs
Deux plaques métalliques verticales (A) et (B) sont placées dans le vide à une distance
Une petite sphère M ponctuelle de masse
On ne peut pas négliger l'action de la pesanteur. Données : Accélération de la pesanteur :
Distance entre les plaques :
Hauteur des plaques :
Rapport charge/masse de la sphère :
|  |
Question
Trouver les deux forces qui agissent sur la petite sphère. Montrer que cette dernière reste dans le plan de la figure
.
Les forces qui agissent sur la sphère sont :
- le poids
- la force électrique
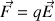
Les deux forces étant dans le plan
, la sphère restera dans ce plan.
Question
En déduire les composantes sur les axes
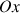et
du vecteur accélération
du mouvement de la sphère.
On applique la deuxième loi de Newton (relation fondamentale de la dynamique) :
L'accélération est :
Les composantes de l'accélération sont :
Les deux composantes de l'accélération sont constantes.
Question
Déterminer, en fonction du temps :
a) Les coordonnées du vecteur vitesse
;
b) Les coordonnées du vecteur position
.
Détermination du vecteur vitesse et du vecteur position.
a) Le vecteur accélération correspond à la variation du vecteur vitesse :
Pour obtenir les coordonnées du vecteur vitesse
, on part des coordonnées du vecteur accélération :
On intègre ensuite les équations différentielles pour trouver les coordonnées du vecteur vitesse :
On doit évaluer les constantes
et
. Les coordonnées du vecteur vitesse doivent être exactes même pour
. D'après la relation ci_dessus, on a :
Or d'après l'énoncé, la sphère est lâchée sans vitesse initiale, soit :
On identifie alors :
Ce qui donne pour les coordonnées du vecteur vitesse :
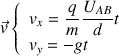
ou :
b) Le vecteur vitesse correspond à la variation du vecteur position :
Pour obtenir les coordonnées du vecteur position
vitesse :
Pour obtenir les coordonnées du vecteur position
, on part des coordonnées du vecteur vitesse :
On intègre les équations différentielles pour trouver les coordonnées du vecteur position :
On doit évaluer les constantes
et
. Les coordonnées du vecteur position doivent être exactes même pour
. D'après la relation ci-dessus, on a :
Or d'après l'énoncé, la sphère est lâchée d'un point
de coordonnées
=
, soit :
On identifie alors :
Ce qui donne pour les coordonnées du vecteur position :
ou :
Question
Écrire l'équation de la trajectoire. Quelle est sa nature ?
Pour écrire l'équation de la trajectoire, il faut éliminer le temps entre les composantes du vecteur position. On a :
On utilise la composante
pour exprimer le temps sous la forme :
On peut alors remplacer le terme
de la composante
par celui que l'on vient d'écrire :
On obtient une expression qui ne dépend plus du temps. On arrange cette expression pour obtenir l'équation de la trajectoire :
Cette expression est de la forme
, c'est donc l'équation d'une droite. La trajectoire de la sphère est rectiligne.
Question
Calculer le temps d'arrivée de la charge dans le plan horizontal passant par
.
Lorsque la sphère se trouve dans le plan horizontal passant par
, on a
. Et on a v que la composante
s'écrit :
soit :
Question
Quelle valeur doit-on donner à
pour que la trajectoire de la charge passe par le point P de cordonnées
?
Si on considère que la trajectoire de la charge passe par le point P de coordonnées
, l'équation de la trajectoire nous donne :
Ce qui est satisfait pour une tension :
