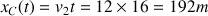Vitesse d'une automobile
Une automobile est arrêtée à un feu rouge. Quand le feu passe au vert, l'automobiliste accélère uniformément pendant un intervalle de temps
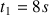avec une accélération constante
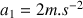suivant une trajectoire rectiligne. Ensuite l'automobiliste se déplace à vitesse constante
.
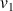Question
Quelles sont la distance parcourue et la vitesse atteinte à la fin de la phase d'accélération ?
L'accélération est constante et vaut
. L'accélération correspond à la variation de la vitesse de l'automobile
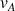suivant la relation :
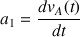
On a après intégration (avec
la constante d'intégration) :
Comme à l'instant initial t=0 l'automobile est à l'arrêt, sa vitesse est nulle, soit
. Or, à l'instant initial
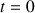, d'après la relation trouvée précédemment, on a
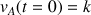. On identifie donc la constante d'intégration à
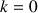. Et l'équation horaire de la vitesse est :
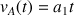
La vitesse correspond à la variation de la position de l'automobile
suivant la relation :
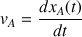
On a après intégration (avec
une nouvelle constante d'intégration) :
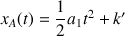
On considère qu'à l'instant initial
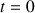l'automobile est à l'arrêt à la position
.
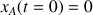Or, à l'instant initial
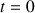, d'après la relation trouvée précédemment, on a
. On identifie donc la constante d'intégration à
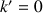. Et l'équation horaire de la position pendant la phase d'accélération est :
La distance parcourue au temps
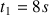vaut :
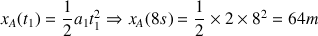
La vitesse atteinte après la phase d'accélération vaut :
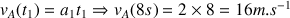
En fin de phase d'accélération, l'automobiliste a atteint la vitesse
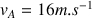. Comme l'énoncé indique que l'automobiliste se déplace ensuite à vitesse constante
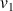, on en conclut que
.
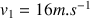L'équation horaire de la trajectoire de l'automobile peut donc s'écrire :
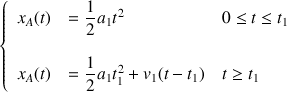
Question
À l'instant du démarrage de l'automobile, un camion la dépasse avec une vitesse constante
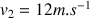. Au bout de combien de temps et à quelle distance du feu l'automobile rattrapera t-elle le camion ?
Le camion n'a pas d'accélération. L'équation horaire de sa vitesse s'écrit simplement :
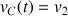
Et l'équation horaire de son mouvement est :
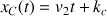
D'après l'énoncé, au moment du démarrage, le camion dépasse l'automobile. On peut donc en conclure qu'à l'instant initial
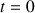, le camion et l'automobile sont au même endroit, c'est-à-dire
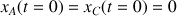, mais le camion ayant une plus grande vitesse (l'automobile a une vitesse nulle au démarrage) il dépasse l'automobile. Comme on a
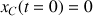, et que pour
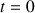l'équation horaire du camion s'écrit
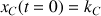, on identifie
. On a donc :
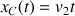
Les deux véhicules ont les équation horaires suivantes :
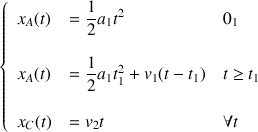
On peut alors tracer la distance parcourue par les deux véhicules en fonction du temps :
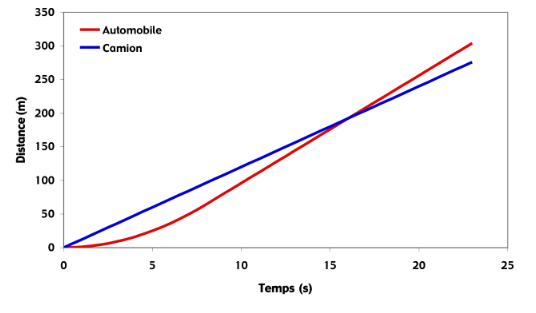
On voit que l'automobile rattrapera le camion pour un temps supérieur à
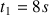. Il faut donc utiliser, pour l'automobile, l'équation horaire pour
.
L'automobile rattrapera le camion lorsqu'elle sera au même endroit
que lui et donc au même instant
. Soit :
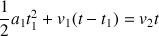
Ce qui donne :
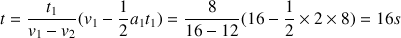
La distance parcourue est donnée par l'une ou l'autre équation horaire :
