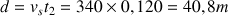Profondeur d'un puits
On lâche une pierre sans vitesse du haut d'un puits. On entend “PLOUF” au temps
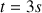après le lâcher. La vitesse du son dans l'air est
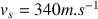. On cherche à calculer la profondeur
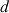du puits jusqu'à l'eau. On prendra
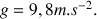
On appellera
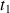la durée de la chute de la pierre et
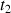la durée de la remontée du son.
Question
Établir l'équation horaire
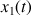de la chute de la pierre. Donner cette relation lorsque la pierre touche l'eau du puits.
La pierre tombe en chute libre du haut du puits pris comme origine d'un repère. L'équation horaire de la trajectoire est :
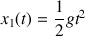
Lorsque la pierre touche l'eau, elle est à la profondeur
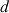au temps
:
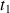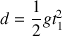
Question
Établir l'équation horaire
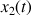de la remontée du son. Donner cette relation lorsque le son arrive en haut du puits.
Le son est émis lorsque la pierre touche l'eau. Ce son remonte à la vitesse du son
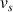. L'équation horaire est alors :
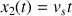
Lorsque le son arrive en haut du puits, il a parcouru la distance
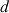en un temps
:
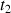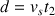
Question
En utilisant une relation liant
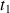et
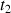, reprenez les deux relations des questions précédentes et calculer :
a) La durée
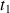de la chute de la pierre ;
b) La durée
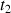de la remontée du son ;
c) La profondeur
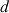du puits.
Le temps
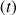écoulé depuis le lâcher de la pierre et l'arrivée à l'eau du puits
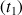puis entre l'émission du bruit et l'arrivée du son au bord du puits
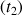est de 3 secondes, c'est-à-dire que :
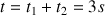
Les distances parcourues par la pierre ou par le son sont les mêmes :
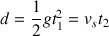
a) Pour la durée
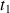de la chute de la pierre, exprimons
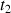en fonction de
:
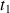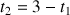
Que l'on utilise dans l'équation (1) :
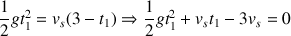
On obtient une équation du second degré que l'on résout de manière classique. On écrit :
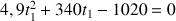
On calcule le discriminant :
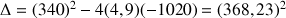
Comme le discriminant n'est ni nul ni négatif, on calcule les deux solutions :
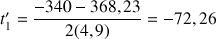
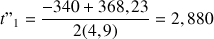
La seule solution convenable est la solution positive, soit :
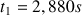
b) Pour la durée
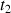de la remontée du son, on a :
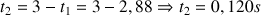
c) Pour la profondeur
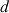du puits, on a :
