Accélération de la Lune
On considère que la Lune tourne autour de la Terre selon un mouvement circulaire. On note
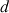la distance Terre–Lune. La période de la Lune, c'est-à-dire le temps que met la Lune pour tourner autour de la Terre, est
.
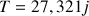Données :
Distance moyenne Terre–Lune :
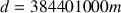
Question
Quelle est la vitesse de rotation
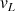de la Lune en m/s et en km/h ?
La Lune parcourt une orbite dont la longueur est donnée par la circonférence :
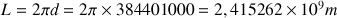
Cette distance est parcourue à la vitesse :
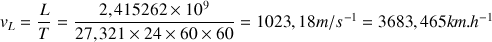
Question
Sur la figure suivante, on a représenté les vecteurs vitesse
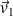et
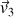lors du mouvement de la Lune autour de la terre. L'intervalle de temps séparant deux points consécutifs est de
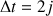
a) Connaissant la vitesse de rotation
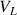(déterminée à la question 1), déterminer l'échelle de la figure : vous donnerez la réponse sous la forme
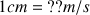
b) Sur cette figure, représenter le vecteur
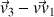au point
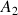
c) Mesurer la longueur du vecteur
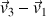, et, avec l'échelle, calculer la valeur de
.
d) En déduire la valeur de l'accélération
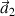au point
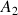
a) La réponse à cette question dépend de la reproduction de la figure et de la précision de la mesure. Pour répondre à cette question il faut mesurer avec une règle graduée la longueur d'un vecteur vitesse (
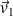ou
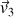) sur le schéma, et de dire que cette longueur correspond à la longueur du vecteur vitesse
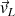. Par exemple, si la mesure donne une longueur
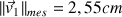, on écrit :
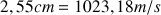
soit une échelle
b) Représentation du vecteur
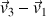au point A2 :
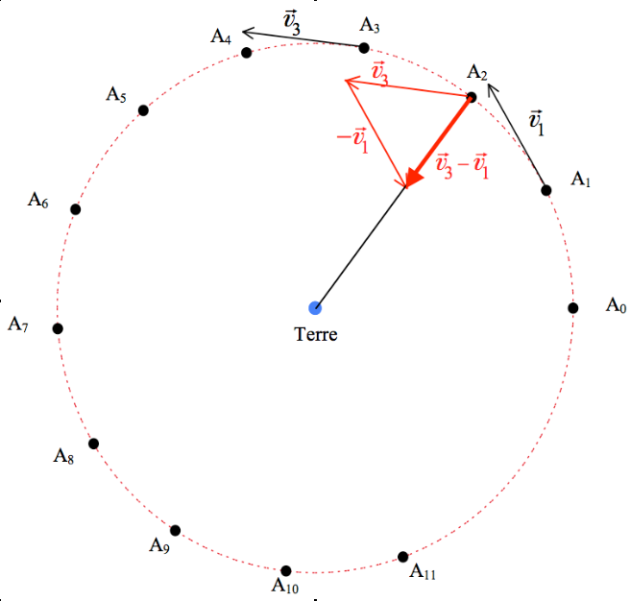
c) Ici aussi, le résultat dépend de la mesure. Mais pour avoir le bon résultat final, lorsque l'on a mesuré
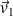ou
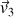à la question 2-a), on doit conserver la même représentation (feuille imprimée par exemple) pour mesurer
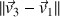. Par exemple, dans les mêmes conditions qu'à la question 2-a). on peut mesurer
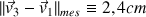. Ainsi :
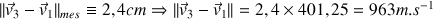
(Remarque : même avec une détermination d'échelle différente à la question 2.a., si les mesures sont bien faites, on doit toujours trouver un résultat pour
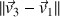proche de
)
d) L'accélération
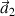au point
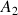est déterminée par la variation de vitesse entre les points
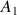et
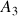, soit sur la variation de vitesse entre deux intervalles de temps
. Ainsi :
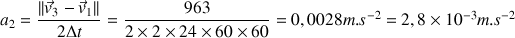
Question
Le mouvement de la Lune est circulaire uniforme.
a) Quelle est dans ce cas la formule qui donne l'accélération
en fonction de la vitesse
et du rayon de courbure
?
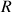b) En prenant le résultat de la question 1, calculer cette accélération.
c) Comparer cette valeur avec celle calculée à la question 2-d).
a) Pour un mouvement circulaire, la relation qui donne l'accélération
en fonction de la vitesse
et de du rayon de courbure
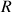est :
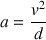
b) Avec
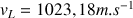, on a :
c) Si on compare avec le résultat de la question 2-d), on remarque que les résultats concordent.
