Chute d'un pot de fleur
Un pot de fleur, de masse
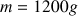, chute verticalement d'un balcon. On repère sa chute par la distance parcourue par le centre d'inertie G du pot de fleur depuis le balcon vers le sol. On effectue l'enregistrement des positions successives de G avec un intervalle de temps
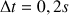entre chaque position. Le schéma suivant, présenté à l'horizontale, donne ces positions depuis l'instant initial
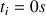(distance parcourue nulle) jusqu'au temps final
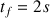(distance parcourue un peu inférieure à 20 m). L'axe horizontal, que l'on considérera comme l'axe
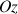, est gradué en mètre et le pot tombe de la position initiale
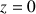; le premier point associé à cette position initiale est noté
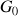(les suivants sont notés
,
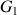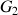, etc).
Question
Étude de la vitesse
a) En vous aidant du quadrillage de la Figure 1, évaluer la vitesse moyenne
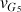du centre d'inertie au point
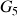
b) Sur le schéma suivant tracer le vecteur vitesse
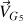à l'échelle
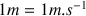( c'est-à-dire qu'une vitesse de
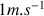doit être représentée par un vecteur de longueur
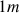en respectant l'échelle de distance du schéma).
Étude de la vitesse.
La qualité des résultats dépend de l'évaluation des distances sur le schéma ; de meilleurs résultats sont obtenus en agrandissant le schéma (zoom de l'écran ou impression papier de grande dimension).
a) La vitesse moyenne du centre d'inertie au point
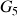s'obtient en calculant la vitesse moyenne entre les points
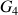et
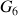. Le schéma permet de déterminer la longueur du segment
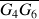. La vitesse moyenne correspond à la distance parcourue de
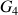et
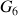pendant deux intervalles de temps :
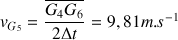
(Les résultats dépendent de la précision des mesures faites sur le schéma : il est normal de trouver des résultats avec une légère différence.)
b) Sur le schéma on doit tracer un qui part de
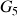et d'une longueur de
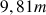suivant l'axe horizontal :
Question
Étude de l'accélération
a) En vous aidant du quadrillage de la figure 1, évaluer les vitesses moyennes
et
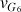du centre d'inertie aux points
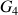et
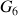b) Calculer la variation de vitesse
entre ces deux points.
c) Calculer la valeur de l'accélération
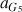en
.
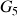d) Sur le schéma suivant tracer le vecteur accélération
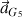à l'échelle
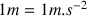( c'est-à-dire qu'une accélération de
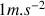doit être représentée par un vecteur de longueur
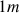en respectant l'échelle de distance du schéma).
e) Que remarquez-vous pour la vitesse et l'accélération du centre d'inertie au point
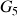? Expliquer cette valeur. Pourquoi est-ce en
?
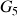f) Quelles devraient être la vitesse et l'accélération du centre d'inertie au point
?
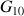Étude de l'accélération.
a) Les vitesses moyennes en
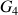et
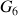s'obtiennent en suivant la méthode de la question 1-a) :
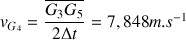
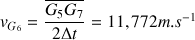
(Les résultats dépendent de la précision des mesures faites sur le schéma : il est normal de trouver des résultats avec une légère différence.)
b) La variation de vitesse entre ces deux points est :
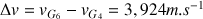
c) L'accélération en
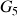s'obtient en divisant la variation de vitesse
entre les positions
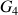et
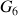par la durée séparant ces deux positions :
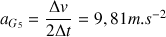
d) Sur le schéma on doit tracer un vecteur qui part de
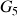et d'une longueur de
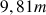suivant l'axe horizontal :
e) La durée de chute du pot de fleur depuis l'origine jusqu'en
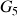est de 1 seconde. On remarque qu'au bout de 1s, la vitesse est de
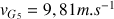et l'accélération de
.
C'est un mouvement de chute libre, l'accélération de centre d'inertie est égale à l'accélération de la pesanteur ; de plus, il n'y a pas de frottement dû à l'air, sinon la valeur de l'accélération serait inférieure à celle de la pesanteur. Cette accélération signifie que la vitesse augmente de
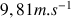chaque seconde. Donc au bout de 1 s, la vitesse doit être de
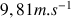, ce qui est effectivement le cas.
f) Il n'est pas possible de calculer la vitesse moyenne au point
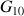, puisque le point
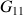n'est pas présent sur le schéma. Néanmoins, comme le point
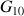correspond à la position du centre d'inertie au bout de 2 secondes, la vitesse atteinte au point
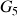est augmentée de
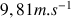; ainsi on peut dire que la vitesse en G10 est :
Dans un mouvement de chute libre sans frottement l'accélération est constante, donc :
Question
Étude des forces.
a) Quelles sont les forces appliquées au pot de fleur ?
b) Calculer la valeur de la somme des forces
appliquées au pot de fleur en
?
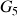c) Quelle st la valeur de
en
?
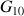Quelle est la nature de ce mouvement ?
Étude des forces.
a) La question 3-e) permet de montrer qu'il n'y a pas de force de frottement. Donc la seule force appliquée au pot de fleur est son poids.
b) On applique la 2ème loi de Newton :
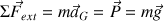
Le mouvement étant linéaire, on a (avec
) :
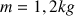c) On a vu à la question 2-f) que l'accélération au point
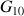doit être
; ainsi :
Le mouvement étudié est un mouvement rectiligne uniformément accéléré.
