Introduction
Durée : 60 minutes
Niveau : moyen
L'aire comprise entre
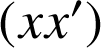 , les deux droites d'équations
, les deux droites d'équations
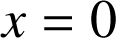 et
et
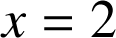 et la courbe
et la courbe
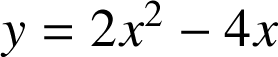 est égale à (choisir la ou les propositions qui conviennent parmi les suivantes) :
est égale à (choisir la ou les propositions qui conviennent parmi les suivantes) :
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Soit
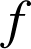 une fonction continue et positive sur un intervalle
une fonction continue et positive sur un intervalle
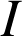 ,
, ![]() sa courbe représentative dans un repère orthogonal,
sa courbe représentative dans un repère orthogonal,
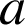 et
et
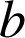 deux éléments de
deux éléments de
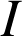 tels que
tels que ![]() . Soit
. Soit
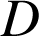 la partie du plan délimitée par la courbe
la partie du plan délimitée par la courbe ![]() , l'axe des abscisses et les droites d'équations respectives
, l'axe des abscisses et les droites d'équations respectives
 et
et
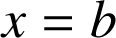 .
.
L'aire, en unités d'aire, de
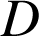 , est appelée intégrale de
, est appelée intégrale de
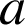 à
à
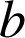 de
de
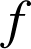 .
.
Cette intégrale se note ![]() .
.
![]() est continue sur
est continue sur
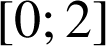 et
et ![]() , pour tout
, pour tout ![]() .
.
Donc l'aire demandée est égale en unités d'aire à : ![]() (réponse 4/) ou
(réponse 4/) ou ![]() (réponse 2/).
(réponse 2/).
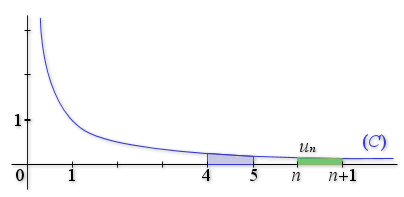
La courbe
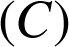 ci-dessous est une partie de la courbe de la fonction
ci-dessous est une partie de la courbe de la fonction ![]() dans un repère orthonormal.
dans un repère orthonormal.
Définition :
Soit
 une fonction continue et positive sur un intervalle
une fonction continue et positive sur un intervalle
 ,
, ![]() sa courbe représentative dans un repère orthogonal,
sa courbe représentative dans un repère orthogonal,
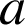 et
et
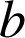 deux éléments de
deux éléments de
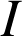 tels que
tels que ![]() . Soit
. Soit
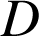 la partie du plan délimitée par la courbe
la partie du plan délimitée par la courbe ![]() , l'axe des abscisses et les droites d'équations respectives
, l'axe des abscisses et les droites d'équations respectives
 et
et
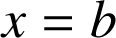 .
.
L'aire, en unités d'aire, de
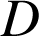 , est appelée intégrale de
, est appelée intégrale de
 à
à
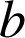 de
de
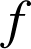 .
.
Cette intégrale se note ![]() .
.
Relation de Chasles :
Soit
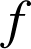 une fonction définie continue sur un intervalle
une fonction définie continue sur un intervalle
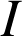 : pour tous réels
: pour tous réels
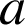 ,
,
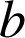 et
et
 de
de
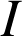 ,
,
1) Déterminer la valeur exacte de l'aire du domaine délimité par
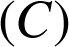 , l'axe des abscisses et les droites d'équations
, l'axe des abscisses et les droites d'équations
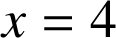 et
et
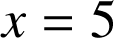 .
.
La fonction inverse ![]() est continue et positive sur
est continue et positive sur
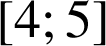 , donc l'aire demandée est égale en unités d'aire à
, donc l'aire demandée est égale en unités d'aire à ![]() , soit
, soit ![]() .
.
2) Soit
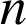 un entier naturel strictement positif. On considère
un entier naturel strictement positif. On considère
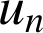 l'aire du domaine situé entre les droites d'équations
l'aire du domaine situé entre les droites d'équations
 et
et
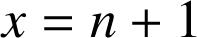 , l'axe des abscisses et la courbe
, l'axe des abscisses et la courbe
 .
.
a. Montrer que 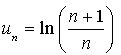 .
.
b. Quelle est la limite de la suite
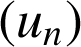 ?
?
a. La fonction inverse ![]() est continue et positive sur
est continue et positive sur
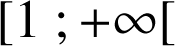 , donc pour tout
, donc pour tout ![]() , .
, .
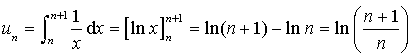
b. 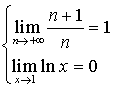 donc
donc 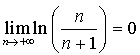 , d'où
, d'où ![]() .
.
3) On pose
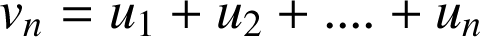 .
.
a. Déterminer un domaine plan dont l'aire est égale à
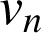 .
.
b. Exprimer
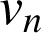 en fonction de
en fonction de
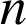 .
.
c. Quelle est la limite de la suite
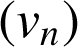 ?
?
a. L'aire en unités d'aire de la partie du plan délimitée par
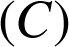 , l'axe des abscisses et les droites d'équation
, l'axe des abscisses et les droites d'équation
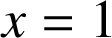 et
et
 est égale à
est égale à
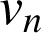 .
.
b. Pour tout ![]() ,
, ![]() , d'où
, d'où ![]() d'après la relation de Chasles.
d'après la relation de Chasles.
On a donc : pour tout ![]() ,
, ![]() .
.
c. 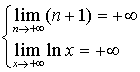 , d'où
, d'où ![]() .
.
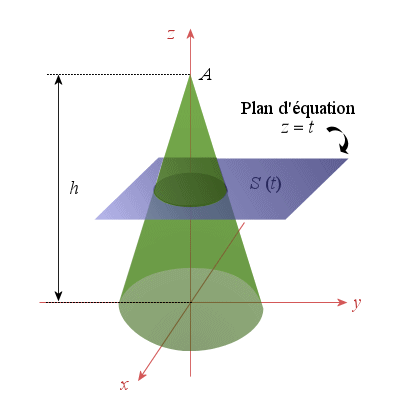
Soit le cône d'axe
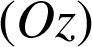 de sommet
de sommet
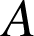 , de hauteur
, de hauteur
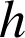 dont la base
dont la base
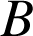 est le disque de centre
est le disque de centre
 et de rayon
et de rayon
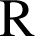 .
.
Tout plan d'équation
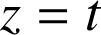 , avec
, avec ![]() , coupe le cône suivant un disque
, coupe le cône suivant un disque
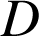 de rayon variable.
de rayon variable.
Théorème fondamental du calcul intégral :
Soient
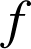 une fonction continue sur un intervalle
une fonction continue sur un intervalle
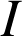 ,
,
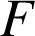 une primitive de
une primitive de
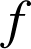 sur
sur
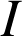 et
et
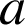 et
et
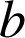 deux réels de
deux réels de
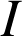 .
. ![]() .
.
On note aussi : ![]() .
.
On pourra considérer la section du cône par le plan
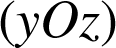 .
.
Reconnaître une situation de Thalès.
1) Déterminer l'aire
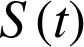 de
de
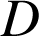 en fonction de
en fonction de
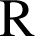 ,
,
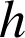 et
et
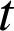 .
.
Considérons la section du cône par le plan
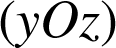 .
.
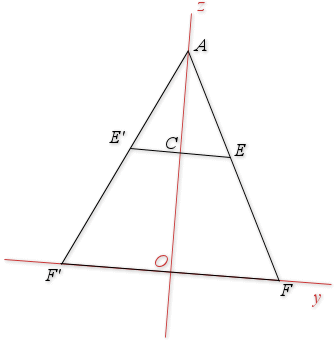
Nous obtenons le triangle
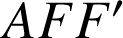 ci-dessus, les points
ci-dessus, les points
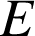 ,
,
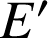 et
et
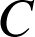 étant des points du plan d'équation
étant des points du plan d'équation
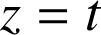 . Dans le triangle
. Dans le triangle
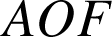 , les droites
, les droites
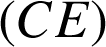 et
et
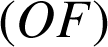 sont parallèles. D'après la propriété de Thalès nous avons :
sont parallèles. D'après la propriété de Thalès nous avons :
![]()
Or ![]() donc
donc ![]() .
.
L'aire en unités d'aire du disque
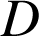 de rayon
de rayon
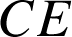 est donc égale à :
est donc égale à : 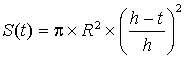 .
.
2) Le volume du cône (en unités de volumes) est donné par la formule ![]() .
.
Calculer
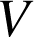 et retrouver le volume du cône en fonction de R et
et retrouver le volume du cône en fonction de R et
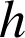 .
.
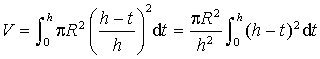 , d'où
, d'où 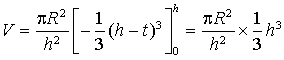 , c'est-à-dire
, c'est-à-dire ![]() en unités de volume.
en unités de volume.






