L'algorithme d'Euclide pour des grandeurs
Calcul de fractions continues
La méthode de retranchement de carrés peut-être appliquée également dans le cas où les côtés
 et
et
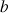 sont incommensurables, c'est-à-dire quand le rapport de leurs mesures est un nombre irrationnel. Le processus de division ne s'arrête donc jamais mais la suite des nombres de carrés retranchés qui apparaissent donnent une suite de très bonnes approximations rationnelles (en un certain sens la meilleure) de ce nombre qui s'appelle le développement en fractions continues.
sont incommensurables, c'est-à-dire quand le rapport de leurs mesures est un nombre irrationnel. Le processus de division ne s'arrête donc jamais mais la suite des nombres de carrés retranchés qui apparaissent donnent une suite de très bonnes approximations rationnelles (en un certain sens la meilleure) de ce nombre qui s'appelle le développement en fractions continues.
Dans l'appliquette suivante, vous pouvez expérimenter en plaçant les points
 et
et
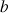 à des coordonnées décimales. Malheureusement les petits carrés deviennent rapidement minuscules et invisibles. Sur la partie droite, l'approximation rationelle associée sous forme de développement en fractions continues.
à des coordonnées décimales. Malheureusement les petits carrés deviennent rapidement minuscules et invisibles. Sur la partie droite, l'approximation rationelle associée sous forme de développement en fractions continues.
Étant donné un nombre réel positif
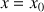 que nous devons approcher. Il a une partie entière
que nous devons approcher. Il a une partie entière
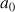 et un reste
et un reste
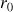 vérifiant
vérifiant
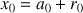 , avec
, avec
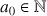 et
et
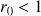 .
.
Si le reste
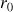 est nul, on arrête et le nombre
est nul, on arrête et le nombre
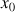 est un entier. Sinon, on calcule
est un entier. Sinon, on calcule
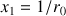 . Ce nombre
. Ce nombre
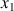 est plus grand que 1 et possède donc une partie entière
est plus grand que 1 et possède donc une partie entière
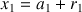 , avec
, avec
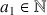 et
et
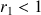 . On obtient ainsi itérativement une suite d'entiers
. On obtient ainsi itérativement une suite d'entiers
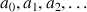 qui est finie si
qui est finie si
 est rationnel, qui donne une suite convergente d'approximations rationnelles dans le cas contraire:
est rationnel, qui donne une suite convergente d'approximations rationnelles dans le cas contraire:
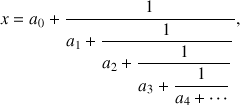
où la limite est à définir proprement.





