L'algorithme d'Euclide et le PGCD
Le plus grand diviseur commun (PGCD) de deux entiers naturels
et
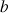est le plus grand nombre qui divise aussi bien
que
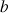. On le notera
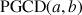. Ce PGCD est important en particulier quand on considère la fraction
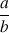car c'est par lui qu'il faut diviser
et
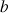pour complètement simplifier la fraction et aucun autre nombre ne convient. Pour deux nombres petits, on peut assez rapidement trouver leur PGCD à la main, mais pour de grands nombres, une approche algorithmique est nécessaire.
L'algorithme d'Euclide est une méthode très efficace. Elle procède par divisions entières successives. Sans perte de généralité, supposons que
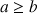. L'idée principale de l'algorithme est la suivante: On divise
par
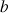ce qui donne un quotient
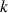et un reste
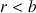vérifiant
.
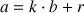Si
,
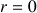est un multiple de
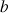et
.
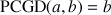Sinon,
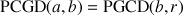car ce qui est commun à
et
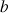le sera également à
.
Comme la suite des restes est strictement décroissante, la procédure récursive s'arrêtera.
Un langage récursif permet une programmation très simple de cet algorithme comme
PGCD(a,b):= {
r=mod(a,b); //Le reste de la division de a par b;
if (r==0)
return b; //On connait le PGCD
else
return PGCD(b,r); //On itère
}
L'appliquette suivante illustre sur le côté droit les divisions entières itérées pour calculer le PGCD des deux nombres
et
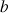controlés par les points horizontaux, resp. verticaux.
La représentation graphique sur le côté gauche donne une interprétation géométrique de l'algorithme d'Euclide. Un rectangle de côtés
et
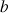est décomposé, le long de son long côté (
) en autant de carrés (de côtés
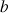) que possible, laissant un rectangle (de côtés
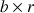). Ce rectangle est lui-même décomposé de la même manière jusqu'au bout. Si les côtés sont des nombres entiers, on obtient ainsi une suite strictement décroissante et le côté du dernier carré, le plus grand avec lequel on peut paver tout le rectangle, est le PGCD.
Ce processus peut s'interpréter en termes complètement géométriques et non plus arithmétiques. Quand l'algorithme s'arrête, cela signifie que les longueurs
et
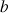sont toutes les deux multiples d'une même longueur, on dit qu'elles sont commensurables. Et leur rapport est un nombre rationnel. Tandis que quand le processus est infini, elles sont incommensurables et leur rapport est un nombre irrationnel.
Un petit exercice: Définissons
le nombre d'or comme le rapport (non entier)
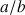vérifiant
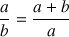. En d'autres termes la longueur
est découpée en deux morceaux tels que le rapport du grand,
, par l'ensemble
est le même que le petit,
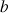, par le grand,
. Soit en construisant le carré de côtés
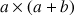, en enlevant un carré de côté
, on obtient un rectangle de même proportion. On voit de suite que ce rapport est irrationnel car l'algorithme d'Euclide ne s'arrête jamais. Une assez bonne approximation rationnelle de ce nombre est 81/50, les approximations précédentes 50/31, 31/19 et 19/12 s'en éloignent ensuite.
