Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
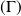le support d'un arc paramétré
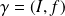de classe
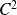dans le plan de repère orthonormé
.
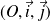Donc :
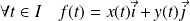, et le point
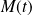a pour coordonnées
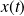et
.
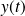Question
Exprimer la courbure
en un point régulier
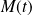en fonction des dérivées des fonctions
et
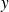par rapport au paramètre
.
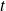Utilisez la dérivée de l'abscisse curviligne.
Soit
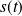une abscisse curviligne du point
.
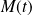Donc :
.
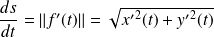Et :
.
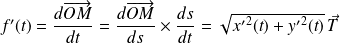Donc le vecteur tangent est :
.
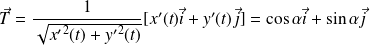Et le vecteur normal est :
.
.
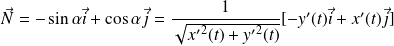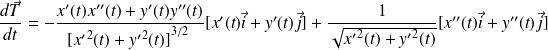Donc :
.
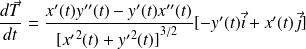Or :
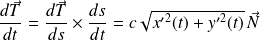où
est la courbure.
Conclusion : La courbure au point
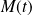est
.
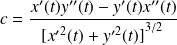Question
Déterminer les arcs paramétrés de classe
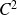et de courbure nulle.
Utilisez l'expression de la courbure
en fonction de
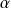, mesure de l'angle
.
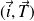N'oubliez pas la réciproque !
Soit
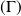une courbe paramétrée dans le plan de repère orthonormé
.
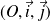Soit
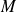un point de
,
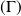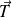le vecteur tangent en
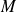et
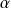une mesure de l'angle
.
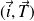La courbure en un point
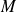est :
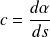en notant
l'abscisse curviligne du point
.
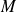Si la courbure
est nulle, alors
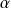est une fonction constante du paramètre
.
Or :
.
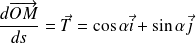Donc il existe deux réels
et
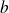tels que :
.
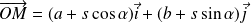Les coordonnées de
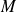sont donc :
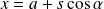, et
.
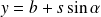Elles vérifient l'équation :
.
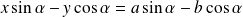Donc la courbe
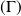est incluse dans une droite.
Réciproquement, supposons que
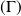soit incluse dans une droite
.
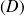Soit
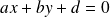une équation de
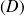avec
.
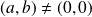Si
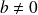, alors
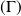est le support d'un arc
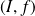avec :
.
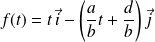Si
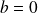, donc
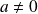, alors
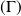est le support d'un arc
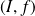avec :
.
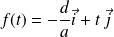Dans les deux cas :
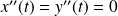. Donc la courbure est :
.
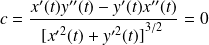Conclusion : La courbure est nulle si et seulement si la courbe est incluse dans une droite.
Question
Déterminer les arcs paramétrés de classe
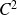et de courbure constante non nulle.
Utilisez l'expression de la courbure
en fonction de
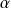, mesure de l'angle
.
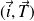N'oubliez pas la réciproque !
On reprend le même raisonnement que dans la question précédente.
Si
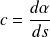est une constante non nulle, on a :
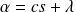où
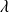est une constante.
Donc :
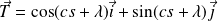. Or :
.
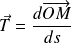Donc il existe deux réels
et
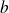tels que :
.
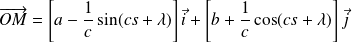Les coordonnées de
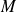sont donc :
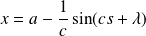et
.
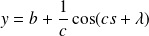Elles vérifient l'équation :
.
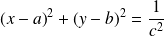Donc la courbe
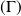est incluse dans un cercle.
Réciproquement, supposons que
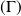soit incluse dans un cercle
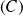de centre
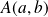et de rayon
.
Une équation de
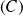est donc :
.
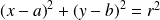Donc
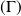est le support d'un arc
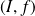avec :
.
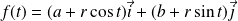Donc :
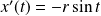, et
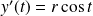, donc :
.
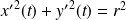D'autre part :
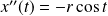, et
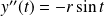, donc :
.
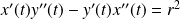Donc la courbure est :
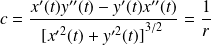. Elle est constante.
Conclusion : La courbure est constante si et seulement si la courbe est incluse dans un cercle.
