Exo 2
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
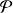 le plan affine euclidien de repère orthomormal
le plan affine euclidien de repère orthomormal
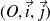 .
.
Soient
 et
et
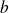 deux réels strictement positifs tels que
deux réels strictement positifs tels que
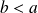 .
.
Soit
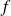 l'application définie sur
l'application définie sur
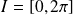 par :
par :
 .
.
Question
Déterminer une équation cartésienne du support
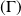 de l'arc
de l'arc
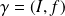 .
.
Eliminez le paramètre
 .
.
Un point
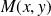 appartient à
appartient à
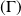 si et seulement si :
si et seulement si :
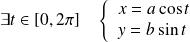 .
.
Donc
 appartient à
appartient à
 si et seulement si :
si et seulement si :
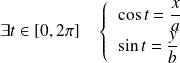 .
.
Conclusion : Une équation cartésienne de
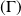 est
est
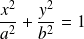 .
.
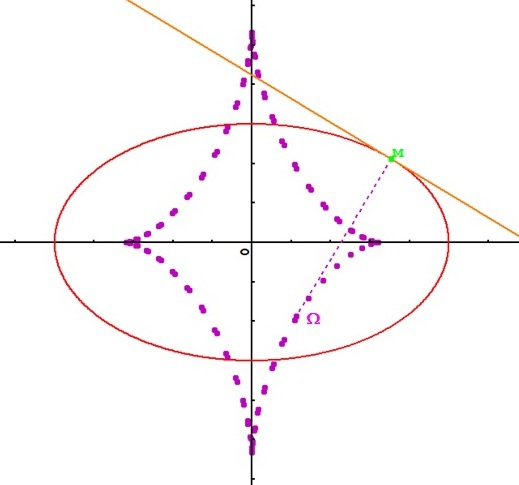
La courbe
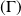 est une ellipse de centre
est une ellipse de centre
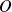 , de grand axe
, de grand axe
 et de petit axe
et de petit axe
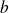 .
.
C'est l'image du cercle de centre
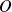 et de rayon
et de rayon
 par l'affinité orthogonale de base l'axe des abscisses et de rapport
par l'affinité orthogonale de base l'axe des abscisses et de rapport
 .
.
Question
Montrer que la courbe
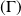 admet en tout point une tangente dont on donnera une équation.
admet en tout point une tangente dont on donnera une équation.
Montrez que tous les points sont réguliers.
L'application
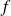 est dérivable sur
est dérivable sur
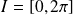 et :
et :
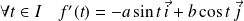 .
.
Or
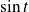 et
et
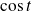 ne s'annulent pas simultanément. Donc :
ne s'annulent pas simultanément. Donc :
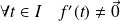 .
.
Donc tous les points de
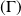 sont réguliers.
sont réguliers.
Donc
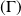 admet une tangente en tout point
admet une tangente en tout point
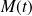 de vecteur directeur
de vecteur directeur
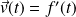 .
.
Soit
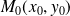 le point de
le point de
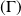 de paramètre
de paramètre
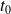 . Donc :
. Donc :
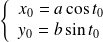 .
.
Le vecteur vitesse en
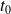 est :
est :
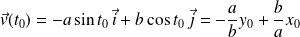 .
.
Un point
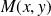 appartient à la tangente si et seulement si :
appartient à la tangente si et seulement si :
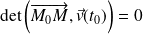 .
.
On obtient :
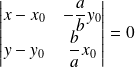 , donc :
, donc :
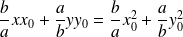 .
.
Conclusion : La courbe
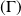 admet en tout point
admet en tout point
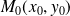 une tangente dont une équation est
une tangente dont une équation est
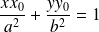 .
.
Question
Déterminer le rayon de courbure et le centre de courbure de
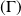 au point
au point
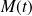 .
.
Utilisez la dérivée de l'abscisse curviligne.
On choisit pour origine sur
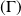 le point
le point
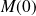 et on note
et on note
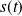 l'abscisse curviligne du point
l'abscisse curviligne du point
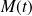 . Donc :
. Donc :
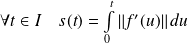 .
.
Donc :
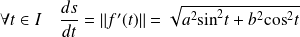 .
.
On détermine le repère de Frenet au point de paramètre
 .
.
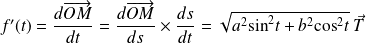 .
.
Donc :
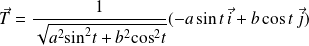 .
.
Et :
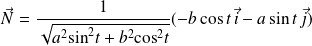 .
.
Soit
 la courbure de
la courbure de
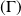 au point
au point
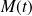 . Donc :
. Donc :
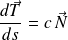 .
.
Donc :
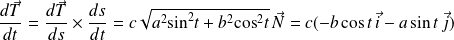 .
.
Or :
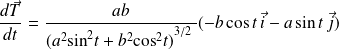 .
.
Donc la courbure au point
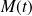 est :
est :
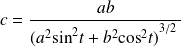 .
.
Or le rayon de courbure est :
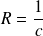 .
.
Conclusion : Le rayon de courbure au point
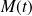 est
est
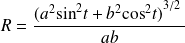 .
.
Et le centre de courbure est le point
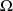 défini par :
défini par :
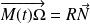 .
.
Donc :
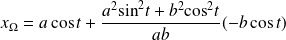 .
.
Et :
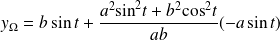 .
.
Conclusion : Le centre de courbure
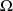 a pour coordonnées
a pour coordonnées
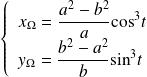 .
.